4.30. A gun can fire shells with maximum speed and the maximum horizontal range that can be achieved is . If a target farther away by distance ∆x has to be hit with the same gun, show that it could be achieved by raising the gun to a height at least
This problem can be approached in two different ways
(i) Refer to the diagram, target T is at a horizontal distance and between the point of projection y = - h.
(ii) From point P in the diagram projection at speed at an angle below horizontal with height h and horizontal range (x)
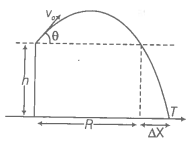
Hint: Time is taken to travel horizontal and vertical distances will be the same.
Step 1: Find the maximum range.
Step 2: Apply equation in the horizontal direction
The horizontal component of initial velocity =
...(ii)
Step 3: Put the value of t in from equation (ii) for vertical motion and calculate h
Let the gun be raised through a height h from the ground so that it can hit the target. Let vertically downward direction is taken as positive
The vertical component of initial velocity
Taking motion in the vertical direction, ...(iii)
Substituting the value of t in Eq. (iii), we get
As the angle of projection is , therefore

© 2026 GoodEd Technologies Pvt. Ltd.