Ncert Exercises & Solutions

4.31. A particle is projected in the air at an angle β to a surface which itself is inclined at an angle α to the horizontal.

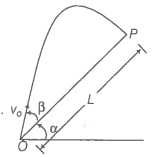
a) find an expression of range on the plane surface

b) time of flight

c) β at which range will be maximum

Hint: Time taken to travel the distances along the inclined plane and perpendicular to the inclined plane will be the same.

Step 1: Consider the adjacent diagram.

Mutually perpendicular x and y-axes are shown in the diagram.
The particle is projected from point O.
Let the time taken in reaching from point O to point P is T.

(b) Step 2: Considering motion along a vertically upward direction perpendicular to OX.

For the journey O to P.
$y = 0, u_{y} = v_{0} \sin β, a_{y} = - g \cos α_{i} t = T$ $y = 0, u_{y} = v_{0} \sin β, a_{y} = - g \cos α_{i} t = T$
Applying equation,

$\begin{array}{l} y = u_{y} t + \frac{1}{2} a_{y} t^{2} \\ \Rightarrow 0 = v_{0} \sin βT + \frac{1}{2} (- gcos α) T^{2} \\ \Rightarrow T [v_{0} \sin β - \frac{gcos α}{2} T] = 0 \end{array}$ $\begin{array}{l} y = u_{y} t + \frac{1}{2} a_{y} t^{2} \\ \Rightarrow 0 = v_{0} \sin βT + \frac{1}{2} (- gcos α) T^{2} \\ \Rightarrow T [v_{0} \sin β - \frac{gcos α}{2} T] = 0 \end{array}$

$\begin{array}{l} \Rightarrow T = 0, T = \frac{2 v_{0} \sin β}{gcos α} \\ As T = 0, corresponding to point O \\ Hence, T = Time of flight = \frac{2 v_{0} \sin β}{gcos α} \end{array}$ $\begin{array}{l} \Rightarrow T = 0, T = \frac{2 v_{0} \sin β}{gcos α} \\ As T = 0, corresponding to point O \\ Hence, T = Time of flight = \frac{2 v_{0} \sin β}{gcos α} \end{array}$

(a) Step 3: Considering motion along OX.

$\begin{array}{l} x = L_{1}, u_{x} = v_{0} \cos β, a_{x} = - gsin α \\ t = T = \frac{2 v_{0} \sin β}{gcos α} \\ x = u_{x} t + \frac{1}{2} a_{x} t^{2} \end{array}$ $\begin{array}{l} x = L_{1}, u_{x} = v_{0} \cos β, a_{x} = - gsin α \\ t = T = \frac{2 v_{0} \sin β}{gcos α} \\ x = u_{x} t + \frac{1}{2} a_{x} t^{2} \end{array}$

$\begin{array}{l} \Rightarrow L = v_{0} \cos βT + \frac{1}{2} (- gsin α) T^{2} \\ \Rightarrow L = v_{0} \cos βT - \frac{1}{2} gsin {αT}^{2} \\ = T [v_{0} \cos β - \frac{1}{2} gsin αT] \\ = T [v_{0} \cos β - \frac{1}{2} gsin α \times \frac{2 v_{0} \sin β}{gcos α}] \\ = \frac{2 v_{0} \sin β}{gcos α} [v_{0} \cos β - \frac{v_{0} \sin αsin β}{\cos α}] \\ = \frac{2 v_{0}^{2} \sin β}{{gcos}^{2} α} [\cos β \cdot \cos α - \sin αsin β] \\ \Rightarrow L = \frac{2 v_{0}^{2} \sin β}{{gcos}^{2} α} \cos (α + β) \end{array}$ $\begin{array}{l} \Rightarrow L = v_{0} \cos βT + \frac{1}{2} (- gsin α) T^{2} \\ \Rightarrow L = v_{0} \cos βT - \frac{1}{2} gsin {αT}^{2} \\ = T [v_{0} \cos β - \frac{1}{2} gsin αT] \\ = T [v_{0} \cos β - \frac{1}{2} gsin α \times \frac{2 v_{0} \sin β}{gcos α}] \\ = \frac{2 v_{0} \sin β}{gcos α} [v_{0} \cos β - \frac{v_{0} \sin αsin β}{\cos α}] \\ = \frac{2 v_{0}^{2} \sin β}{{gcos}^{2} α} [\cos β \cdot \cos α - \sin αsin β] \\ \Rightarrow L = \frac{2 v_{0}^{2} \sin β}{{gcos}^{2} α} \cos (α + β) \end{array}$

$\begin{array}{l} Let, Z = \sin β \cdot \cos (α + β) \\ = \sin β [\cos α \cdot \cos β - \sin α \cdot \sin β] \\ = \frac{1}{2} [\cos α \cdot \sin 2 β - 2 \sin α \cdot \sin^{2} β] \\ = \frac{1}{2} [\sin 2 β \cdot \cos α - \sin α (1 - \cos 2 β)] \\ \Rightarrow z = \frac{1}{2} [\sin 2 β \cdot \cos α - \sin α + \sin α \cdot \cos 2 β] \\ = \frac{1}{2} [\sin 2 β \cdot \cos α + \cos 2 β \cdot \sin α - \sin α] \\ = \frac{1}{2} [\sin (2 β + α) - \sin α] \end{array}$ $\begin{array}{l} Let, Z = \sin β \cdot \cos (α + β) \\ = \sin β [\cos α \cdot \cos β - \sin α \cdot \sin β] \\ = \frac{1}{2} [\cos α \cdot \sin 2 β - 2 \sin α \cdot \sin^{2} β] \\ = \frac{1}{2} [\sin 2 β \cdot \cos α - \sin α (1 - \cos 2 β)] \\ \Rightarrow z = \frac{1}{2} [\sin 2 β \cdot \cos α - \sin α + \sin α \cdot \cos 2 β] \\ = \frac{1}{2} [\sin 2 β \cdot \cos α + \cos 2 β \cdot \sin α - \sin α] \\ = \frac{1}{2} [\sin (2 β + α) - \sin α] \end{array}$

Step 5: For z to be maximum

$\begin{array}{l} \sin (2 = β + α) = maximum = 1 \\ \Rightarrow 2 β + α = \frac{π}{2} or, β = \frac{π}{4} - \frac{α}{2} \end{array}$ $\begin{array}{l} \sin (2 = β + α) = maximum = 1 \\ \Rightarrow 2 β + α = \frac{π}{2} or, β = \frac{π}{4} - \frac{α}{2} \end{array}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions