Question 5.16:
Two masses 8 kg and 12 kg are connected at the two ends of a light inextensible string that goes over a frictionless pulley. Find the acceleration of the masses and the tension in the string when the masses are released.
The given system of two masses and a pulley can be represented as shown in the following figure:
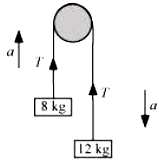
Smaller mass, = 8 kg
Larger mass, = 12 kg
Tension in the string = T
Mass , owing to its weight, moves downward with acceleration a, and mass moves upward.
Applying Newton’s second law of motion to the system of each mass:
For mass : The equation of motion can be written as:
T – g = ma …………… (i)
For mass : The equation of motion can be written as:
Adding equations (i) and (ii), we get:
Therefore, the acceleration of the masses is 2 m/s2.
Substituting the value of a in equation (ii), we get:
Therefore, the tension in the string is 96 N.

© 2026 GoodEd Technologies Pvt. Ltd.