A uniform cube of mass \(m\) and side \(a\) is placed on a frictionless horizontal surface. A vertical force \(F\) is applied to the edge as shown in the figure. Match the following (most appropriate choice).

| List- I | List- II | ||
| (a) | \(mg/4<F<mg/2\) | (i) | cube will move up. |
| (b) | \(F>mg/2\) | (ii) | cube will not exhibit motion. |
| (c) | \(F>mg\) | (iii) | cube will begin to rotate and slip at \(A\). |
| (d) | \(F=mg/4\) | (iv) | normal reaction effectively at \(a/3\) from \(A\), no motion. |
| 1. | a - (i), b - (iv), c - (ii), d - (iii) |
| 2. | a - (ii), b - (iii), c - (i), d - (iv) |
| 3. | a - (iii), b - (i), c - (ii), d - (iv) |
| 4. | a - (i), b - (ii), c - (iv), d - (iii) |
Consider the given diagram, the moment of the force \(F\) about point \(A,\) \(τ _1 = r\times F\) (anti-clockwise)
The moment of weight \(mg\) of the cube about point \(A.\)
\(τ _2 = mg × \frac{a}{ 2}\)
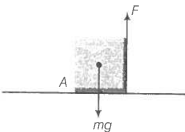
Step 2: Equate the torques for no motion and find the value of \(F.\)
( In this case, both the torque will cancel the effect of each other)
\(F × a = mg × \frac{a}{ 2} ⇒ F = \frac{mg}{ 2}\)
Step 3: Find the value of \(F\) for which the cube will rotate.
Cube will rotate only when, \(𝜏 _1 > 𝜏 _2\)
\(⇒ F × a > mg × \frac{a} {2} ⇒ F > \frac{mg} {2}\)
Step 4: If the normal reaction is acting at \(a/3\) from point \(A\) and for no motion find \(F\) and interpret.
Let the normal reaction is acting at \(a/3\) from point \(A,\) then
\(mg × \frac{a}{ 3} = F × a~\text{ or }~ F = \frac{mg}{ 3} \)
When \(F = \frac{mg}{ 4},\)
there will be no motion.
Hence, option (2) is the correct answer.

© 2026 GoodEd Technologies Pvt. Ltd.