Q.18 A uniform sphere of mass m and radius R is placed on a rough horizontal surface (figure). The sphere is struck horizontally at a height h from the floor. Match the following
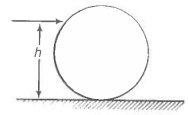
(a) h = R/2 (i) Sphere rolls without slipping with a constant velocity and no loss of energy.
(b) h = R (ii) Sphere spins clockwise, loses energy by friction.
(c) h = 3R/2 (iii) The sphere spins anti-clockwise, loses energy by friction.
(d) h = 7R/5 (iv) Sphere has only a translational motion, loses energy by friction.

© 2026 GoodEd Technologies Pvt. Ltd.