Answer the following:
(a) The casing of a rocket in flight burns up due to friction. At whose expense is the heat energy required for burning obtained? The rocket or the atmosphere?
(b) Comets move around the sun in highly elliptical orbits. The gravitational force on the comet due to the sun is not normal to the comet’s velocity in general. Yet the work done by the gravitational force over every complete orbit of the comet is zero. Why?
(c) An artificial satellite orbiting the earth in a very thin atmosphere loses its energy gradually due to dissipation against atmospheric resistance, however small. Why then does its speed increase progressively as it comes closer and closer to the earth?
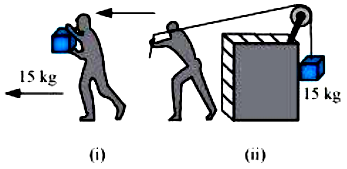
(d) In Fig. 6.13(i) the man walks 2 m carrying a mass of 15 kg on his hands. In Fig. 6.13(ii), he walks the same distance pulling the rope behind him. The rope goes over a pulley, and a mass of 15 kg hangs at its other end. In which case is the work done greater?
(a) Heat energy required for burning of casing of the rocket comes from the rocket itself. As
a result of work done against friction the kinetic energy of the rocket continuously decreases – and this work against friction reappears as heat energy.
(b) This is because the gravitational force is a conservative force. Work done by the gravitational ‘ force of the sun over a closed path in every complete orbit of the comet is zero.
(c) As an artificial satellite gradually loses its energy due to dissipation against atmospheric resistance, its potential decreases rapidly. As a result, kinetic energy of
satellite slightly increases i.e., its speed increases progressively.
(d) In Fig. (i), force is applied on the mass, by the man in vertically upward direction but distance is moved along the horizontal.
θ = 90°. W = Fs cos 90° = zero
In Fig. (ii), force is applied along the horizontal and the distance moved is also along the horizontal. Therefore, θ = 0°.
W = Fs cos θ = mg x s cos 0°
W = 15 x 9.8 x 2 x 1 = 294 joule.
Thus, work done in (ii) case is greater.

© 2026 GoodEd Technologies Pvt. Ltd.