Ncert Exercises & Solutions

A ball of mass m, moving with a speed $2 v_{0}$ $2 v_{0}$ , collide inelastically (e > 0) with an identical ball at rest. Show that

(a) For head-on collision, both the balls move forward.
(b) For a general collision, the angle between the two velocities of scattered balls is less than 90 $°$ $°$ .

Hint: Use the Principle of conservation of linear momentum.

Step 1: Find velocities of the balls after collision by applying momentum conservation and the equation of eccentricity.

(a) Let $v_{1} and v_{2}$ $v_{1} and v_{2}$ are velocities of the two balls after the collision.
Now bv the Principle of conservation of linear momentum.

$\begin{array}{l} 2 {mv}_{0} = {mv}_{1} + {mv}_{2} \\ or 2 v_{0} = v_{1} + v_{2} \\ and e = \frac{v_{2} - v_{1}}{2 v_{0}} \\ \Rightarrow v_{2} = v_{1} + 2 v_{0} e \\ ∴ 2 v_{1} = 2 v_{0} - 2 {ev}_{0} \\ ∴ v_{1} = v_{0} (1 - e) \end{array}$ $\begin{array}{l} 2 {mv}_{0} = {mv}_{1} + {mv}_{2} \\ or 2 v_{0} = v_{1} + v_{2} \\ and e = \frac{v_{2} - v_{1}}{2 v_{0}} \\ \Rightarrow v_{2} = v_{1} + 2 v_{0} e \\ ∴ 2 v_{1} = 2 v_{0} - 2 {ev}_{0} \\ ∴ v_{1} = v_{0} (1 - e) \end{array}$

Since $e < 1 \Rightarrow v_{1}$ $e < 1 \Rightarrow v_{1}$ , has the same sign as $v_{0}$ $v_{0}$ , therefore, the ball moves on after collision.

Step 2: Interpret the (b) part.

(b) Consider the diagram below for a general collision.

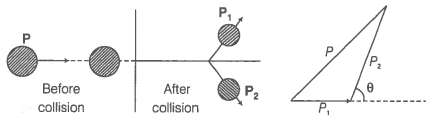
By the principle of conservation of linear momentum,

$P = P_{1} + P_{2}$ $P = P_{1} + P_{2}$

For inelastic collision, some KE is lost, hence

$\frac{p^{2}}{2 m} > \frac{p_{1}^{2}}{2 m} + \frac{p_{2}^{2}}{2 m}$ $\frac{p^{2}}{2 m} > \frac{p_{1}^{2}}{2 m} + \frac{p_{2}^{2}}{2 m}$
$∴ p^{2} > p_{1}^{2} + p_{2}^{2}$ $∴ p^{2} > p_{1}^{2} + p_{2}^{2}$

Thus, $p, p_{1} and p_{2}$ $p, p_{1} and p_{2}$ are related as shown in the figure.

$θ is acute (less than 90^{\circ}) (p^{2} = p_{1}^{2} + p_{2}^{2} would given θ = 90^{\circ})$ $θ is acute (less than 90^{\circ}) (p^{2} = p_{1}^{2} + p_{2}^{2} would given θ = 90^{\circ})$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions