Question 6.25:
Two inclined frictionless tracks, one gradual and the other steep meet at A from where two stones are allowed to slide down from rest, one on each track (Fig. 6.16). Will the stones reach the bottom at the same time? Will they reach there at the same speed? Explain. , and h = 10 m, what are the speeds and times taken by the two stones?
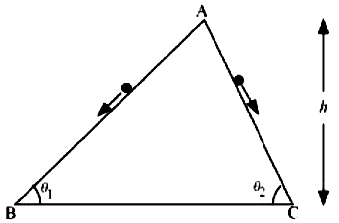
No; the stone moving down the steep plane will reach the bottom first Yes; the stones will reach the bottom with the same speed
The given situation can be shown as in the following figure:
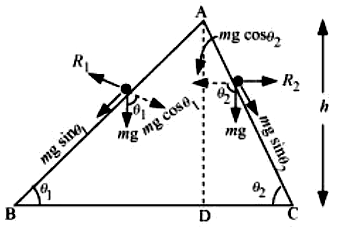
Here, the initial height (AD) for both the stones is the same (h). Hence, both will have the same potential energy at point A.
As per the law of conservation of energy, the kinetic energy of the stones at points B and C will also be the same, i. e.,
Hence, both stones will reach the bottom with the same speed, v
For stone I:
Net force acting on this stone is given by:
For stone II:
Using the first equation of motion, the time of slide can be obtained as:
For stone I:
For stone II:
Hence, the stone moving down the steep plane will reach the bottom first.
The speed (v) of each stone at points B and C is given by the relation obtained from the law of conservation of energy.

© 2026 GoodEd Technologies Pvt. Ltd.