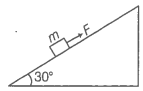
Q.44 A block of mass 1 kg is pushed up a surface inclined to horizontal at an angle of 30 by a force of 10 N parallel to the inclined surface (figure). The coefficient of friction between the block and the incline is 0.1. If the block is pushed up by 10 m along the incline, calculate
(a) work done against gravity
(b) work done against force of friction
(c) increases in potential energy
(d) increase in kinetic energy
(e) work done by applied force
Consider the adjacent diagram, the block is pushed up by applying a force F.

Normal reaction (N) and frictional force (f) is shown.
Given, mass 1 kg.
F = 10 N, = 0.1 and s = distance moved by the block along the inclined plane 10 m
(a) Work done against gravity = Increase in potential energy of the block
Step 2: Find work done against friction
(b) Work done against friction
Step 3: Find increase in potential energy.
(c) increase in potential energy = mgh = mg (s sin )
Step 3: Find the change in kinetic energy.
(d) By work-energy theorem, we know that work done by all the forces = change in KE
Step 4: Find work done by the applied force.
(e) Work done by the applied force, F = FS
= (10)(10) = 100J

© 2026 GoodEd Technologies Pvt. Ltd.