Ncert Exercises & Solutions

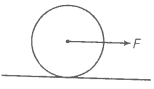
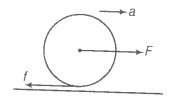
Q. 28 A uniform disc of radius R, is resting on a table on its rim. coefficient of friction between disc and table is $μ$ (figure). Now, the disc is pulled with a force F as shown in the figure. What is the maximum value of F for which the disc rolls without slipping?

Hint: for pure rolling

α = a / R .

Step 1: Write the equation for translational motion.

Consider the diagram below
Frictional force (f) is acting in the opposite direction of
Let the acceleration of the center of mass to disc a then

F - f = Ma ...(i)
where M is the mass of the disc

Step 2: Write the equation for pure rolling.
The angular acceleration of the disc is

\begin{array}{l} α = a / R (for pure rolling) \\ Step 3 : Write the equation for torque . \\ from τ = lα \\ \Rightarrow fR = (\frac{1}{2} {MR}^{2}) α \Rightarrow fR = (\frac{1}{2} {MR}^{2}) (\frac{a}{R}) \\ \Rightarrow Ma = 2 f . . . (ii) \end{array}

Step 4: Find

F_{\max} by soving the equations .

from equations (i) and (ii), we get

f = F / 3 [∵ N = Mg]

∵ f \leq μN = μMg

\Rightarrow \frac{F}{3} \leq μMg \Rightarrow F \leq 3 μMg

\Rightarrow F_{\max} = 3 μMg

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions