Q.24 Consider a long steel bar under tensile stress due to force F acting at the edges along the length of the bar (figure). Consider a plane making an angle with the length. What are the tensile and shearing stresses on this plane?
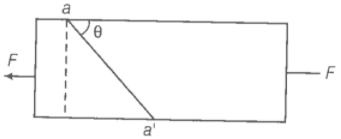
(a) For what angle is the tensile stress a maximum?
(b) For what angle is the shearing stress a maximum?

© 2026 GoodEd Technologies Pvt. Ltd.