Ncert Exercises & Solutions

Q.26. A steel rod of length 2l, cross-sectional area A and mass M is set rotating in a horizontal plane about an axis passing through the centre. If Y is Young's modulus for steel, find the extension in the length of the rod. (assume the rod is uniform)

Hint: The centrifugal force in the rod produces strain in the rod.

Step 1: Find the tension in the rod.

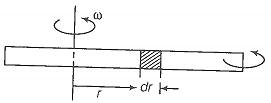
Consider an element of width dr at r as shown in the diagram.

Let T(r) and T(r+dr) be the tensions at r and r+dr respectively.

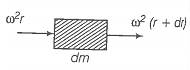
Net centrifugal force on the element

$= ω^{2} r d m$ (where

$ω$ is the angular velocity of the rod)

$= ω^{2} r μ d r$

$(∵ μ = mass/length)$

$\Rightarrow$

$T (r) - T (r + d r) = μ ω^{2} r d r$

$\Rightarrow$

$- d T = μ ω^{2} r d r$
[

$∵$ Tension and centrifugal forces are opposite]

$∴$

$- \int_{T = 0}^{T} d T = \int_{r = l}^{r = r} μ ω^{2} r d r$

$[∵ T = 0 at r = l]$

$\Rightarrow$

$T (r) = \frac{μ ω^{2}}{2} (l^{2} - r^{2})$

Step 2: Find the strain produced in the rod.

Let the increase in length of the element dr be

$Δ r$ .

So, Young's modulus,

$Y = \frac{Stress}{Strain} = \frac{T (r) / A}{\frac{Δ r}{d r}}$

$∴ \frac{Δ r}{d r} = \frac{T (r)}{Y A} = \frac{μ ω^{2}}{2 Y A} (l^{2} - r^{2})$

$∴ Δ r = \frac{1}{Y A} \frac{μ ω^{2}}{2} (l^{2} - r^{2}) d r$

$∴$

$∆$ = change in length in right part =

$\frac{1}{Y A} \frac{μ ω^{2}}{2} \int_{0}^{l} (l^{2} - r^{2}) d r$

$= (\frac{1}{Y A}) \frac{μ ω^{2}}{2} [l^{3} - \frac{l^{3}}{3}] = \frac{1}{3 Y A} μ ω^{2} l^{2}$

$∴$ Total change in length

$= 2 Δ = \frac{2}{3 Y A} μ ω^{2} l^{2}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions