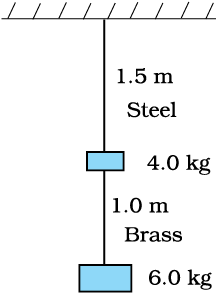
The total force exerted on the steel wire = F${}_1$ = (4 + 6) g = 10 × 9.8 = 98 N

Young’s modulus of steel ${\mathrm{Y}}_1=2.0\times {10}^{11}\mathrm{Pa}$

Change in length of the steel wire:

$$
$∆{\mathrm{L}}_1=\frac{{\mathrm{F}}_1\times {\mathrm{L}}_1}{{\mathrm{A}}_1\times {\mathrm{Y}}_1}=\frac{{\mathrm{F}}_1\times {\mathrm{L}}_1}{{{\mathrm{\pi r}}_1}^2\times {\mathrm{Y}}_1}$
$=\frac{98\times 1.5}{\mathrm{\pi }(0.125\times {10}^{-2})\times 2\times {10}^{11}}=1.49\times {10}^{-4} \mathrm{m}$

The total force on the brass wire = F${}_2$=6 ×9.8=58.8N

Young’s modulus for brass:

${\mathrm{Y}}_2=0.91\times {10}^{11} \mathrm{N}/{\mathrm{m}}^2$

Change in length of the brass wire:

$$
$∆{\mathrm{L}}_2=\frac{{\mathrm{F}}_2\times {\mathrm{L}}_2}{{\mathrm{A}}_2\times {\mathrm{Y}}_2}=\frac{{\mathrm{F}}_2\times {\mathrm{L}}_2}{{\mathrm{\pi r}}_2^2\times {\mathrm{Y}}_2}$
$=\frac{58.8\times 1.0}{\mathrm{\pi }\times {(0.125\times {10}^{-2})}^2\times (0.91\times {10}^{11})}=1.3\times {10}^{-4} \mathrm{m}$

Elongation of the steel wire = 1.49 × 10${}^{-4}$ m

Elongation of the brass wire = 1.3 × 10${}^{-4}$ m

9.6 The edge of an aluminium cube is 10 cm long. One face of the cube is firmly fixed to a vertical wall. A mass of 100 kg is then attached to the opposite face of the cube. The shear modulus of aluminium is 25 GPa. What is the vertical deflection of this face?

It is given in the question that:

Shear modulus (η) of aluminium = 25 GPa = 25 × 10${}^9$ Pa 

Shear modulus, (η)=$=\frac{\mathrm{Shear} \mathrm{stress}}{\mathrm{Shear} \mathrm{strain}}=\frac{{\displaystyle \frac{\mathrm{F}}{\mathrm{A}}}}{{\displaystyle \frac{\mathrm{L}}{∆\mathrm{L}}}}$

Area of the cube, A = Area of one of the faces of the cube = 0.1 × 0.1 = 0.01 m${}^2$

Vertical deflection of the cube,

$∆\mathrm{L}=\frac{\mathrm{FL}}{\mathrm{An}}$
$=\frac{980\times 0.1}{{10}^{-2}\times (25\times {10}^9)}$
$=3.92\times {10}^{-7} \mathrm{m}$

The vertical deflection of this face of the cube is $3.92\times {10}^{-6} \mathrm{m}$.