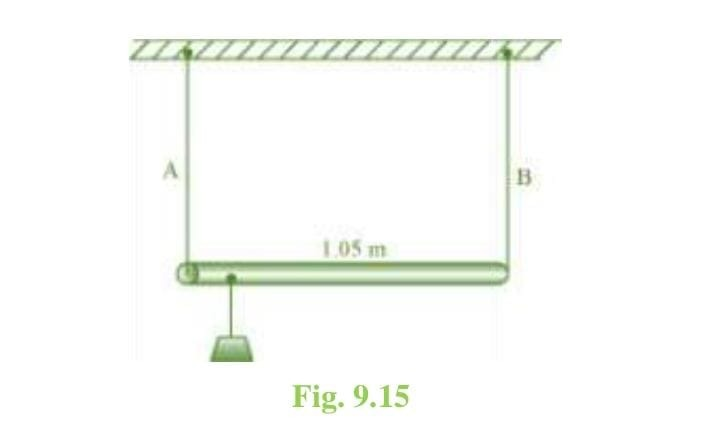
9.18 A rod of length 1.05 m having negligible mass is supported at its ends by two wires of steel (wire A) and aluminium (wire B) of equal lengths as shown in Fig. 9.15. The cross-sectional areas of wires A and B are 1.0 mm2 and 2.0 mm2, respectively. At what point along the rod should a mass m be suspended in order to produce (a) equal stresses and (b) equal strains in both steel and aluminium wires.
(a)
Given that:
Cross-sectional area of wire A, = 1.0 mm = 1.0 × m
Cross-sectional area of wire B, = 2.0 mm = 2.0 × 10 m
Young’s modulus for steel, Y = 2.0 × 10 Nm
Young’s modulus for aluminium, = 7.0 × Nm
Let a small mass m is suspended to the rod at a distance x from the end where wire A is attached.
When the two wires have equal stresses,
...............(i)
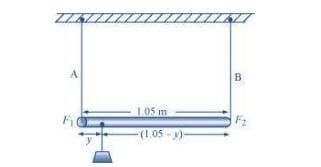
Taking torque about the point of suspension,
Using equations (i) and (ii),
In order to produce equal stress in both of the wires, the mass should be suspended at a distance of 0.7 m from the end where wire A is attached.
(b)
Young's modulus =
If the strain in the two wires is equal,
Let a mass m is suspended at a distance from the side where wire A attached.
Taking torque about the point where mass m is suspended,
Using equations (iii) and (iv),
In order to produce an equal strain in the two wires, the mass should be suspended at a distance of 0.432 m from the end where wire A is attached.

© 2026 GoodEd Technologies Pvt. Ltd.