Ncert Exercises & Solutions

Q. 15 A cubical block of density $ρ$ is floating on the surface of the water. Out of its
height L, fraction x is submerged in water. The vessel is in an elevator
accelerating upward with acceleration a. What is the fraction immersed?

Hint: The pseudo acceleration acts on both the block and the water.

Step 1: Find the initial part of the block submerged in water.

Consider the diagram.

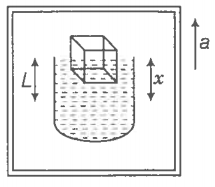
Let the density of water be

ρ_{w}

and a cubical block of ice of side L be floating in water with x of its height (L) submerged in water.

The volume of the block, (V)=

L^{3}

Mass of the block, (m) =

V ρ = L^{3} ρ

Weight of the block, W = mg =

L^{3} ρ g

Case 1:
The volume of the water displaced by the submerged part of the block =

x L^{2}

∴

Weight of the water displaced by the block = x

L^{2} ρ_{w} g

In floating condition,

Weight of the block = Weight of the water displaced by the block

L^{3} ρ g = x L^{2} ρ_{w} g

\frac{x}{L} = \frac{ρ}{ρ_{w}}

Step 2: Find the final fraction of the block submerged in water.

Case 2:
When the elevator is accelerating upward with an acceleration a, then effective acceleration=(g + a)

(∵

Pseudo force is downward

)

Then, the weight of the block =m(g + a)

L^{3} ρ (g + a)

Let x' fraction be submerged in water when the elevator is accelerating upwards.
Now, in the floating condition, the weight of the block = weight of the displaced water

L^{3} ρ (g + a) = (x' L^{2}) ρ_{w} (g + a)

\frac{x'}{L} = \frac{ρ}{ρ_{w}}

From the 1st and 2nd case, we see that the fraction of the block submerged in water is independent of the acceleration of the elevator.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions