Ncert Exercises & Solutions

Q. 21 (a) Pressure decreases as one ascends the atmosphere. If the density of air is $ρ$ , what is the change in pressure dp over a differential height dh?

(b) Considering the pressure p to be proportional to the density, find the p at a height h if the pressure on the surface of the earth is $p_{o}$ .

(c) If $p_{o} = 1.03 \times 10^{3} {Nm}^{- 2}, ρ_{o} = 1.29 {kgm}^{- 3} and g = 9.8 m / s^{2}$ , at what height will be pressure drop to (1/10) the value at the surface of the earth?

(d) This model of the atmosphere works for relatively small distances. Identify the underlying assumption that limits the model.

Hint: The upthrust of the underlying air balances the weight of the upper air.

Step 1: Find the pressure difference at height h.

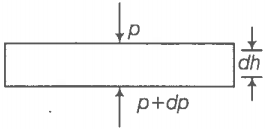
(a) Consider a horizontal parcel of air with cross-section A and height dh.

Let the pressure on the top surface and bottom surface be P and P+dP. If the parcel is in equilibrium, then the net upward force must be balanced by the weight.

i.e. (P+dp)A - PA =—

$ρ$ gAdh (.: Weight = Density x Volume x g)

$\Rightarrow dp = - ρgdh (ρ = density of air)$

The negative sign shows that the pressure decreases with height.

Step 2: Find the equation of pressure at height h.

(b) Let

$ρ_{0}$ be the density of air on the surface of the earth.
As per the question, pressure

$\propto$ density

$\Rightarrow \frac{P}{P_{o}} = \frac{ρ}{ρ_{o}}$

$\Rightarrow ρ = \frac{ρ_{o}}{P_{o}} P$

$∴ dp = - \frac{ρ_{o} g}{P_{o}} Pdh [∵ dp = - pgdh]$

$\Rightarrow \frac{dp}{P} = - \frac{ρ_{o} g}{P_{o}} dh$

$\Rightarrow \int_{P_{o}}^{P} \frac{dp}{P} = - \frac{ρ_{o} g}{P_{o}} \int_{0}^{h} dh [∵ at h = 0, P = P_{o} and at h = h, P = P]$

$\Rightarrow In \frac{P}{P_{o}} = - \frac{ρ_{o} g}{P_{o}} h$

By removing log,

$P = P_{o} e^{(- \frac{ρ_{o} gh}{P_{o}})}$

Step 3: Find the height h for the required pressure using the equation of pressure at height h.

$P_{o} e^{(- \frac{ρ_{o} gh}{P_{o}})},$

$\Rightarrow \ln (\frac{\frac{1}{10} P_{o}}{P_{o}}) = - \frac{ρ_{o} g}{P_{o}} h$

$\Rightarrow \ln (\frac{1}{10}) = - \frac{ρ_{o} g}{P_{o}} {hρ}_{o}$

$∴ h = - \frac{P_{o}}{ρ_{o} g} \ln (\frac{1}{10}) = - \frac{P_{o}}{ρ_{o} g} In {(10)}^{- 1} = \frac{P_{o}}{ρ_{o} g} \ln (10)$

$= \frac{P_{o}}{ρ_{o} g} \times 2.303 [∴ In (x) = 2.303 \log_{10} (x)]$

$= \frac{1.013 \times 10^{5}}{1.22 \times 9.8} \times 2.303 = 0.16 \times 10^{5} m$

$= 16 \times 10^{3} m$

_{(d) We know that $P \propto p$ (When T=constant i.e. isothermal pressure)}

_{Temperature (T) remains constant only near the surface of the earth, not at the greater heights.}

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions