10.31 (a) It is known that density ρ of air decreases with height y as:
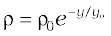
where ρ0 = 1.25 kg m–3 is the density at sea level and is a constant. This density variation is called the law of atmospheres. Obtain this law assuming that the temperature of the atmosphere remains a constant (isothermal conditions). Also, assume that the value of g remains constant.
(b) A large He balloon of volume 1425 m3 is used to lift a payload of 400 kg. Assume that the balloon maintains constant radius as it rises. How high does it rise?
[Take y0 = 8000 m and = 0.18 kg m–3].
(a)
Consider a layer of thickness dy at the height y and cross-section area A.
Mass of the layer = Mass of the atoms in the layer
(b)

© 2026 GoodEd Technologies Pvt. Ltd.