charges placed at points A and B are represented in the given figure. O is the midpoint of the line joining the two charges.

Magnitude of charge located at A, q = 1.5 uC Magnitude of charge 1SuC
located at B, q2 2.5 $\mathrm{\mu }$C

Distance between the two charges, d= 30 cm= 0.3 m

(a) Let Vi and Es are the electric potentials and electric field respectively at O.

Vi = Potential due to charge at A + Potential due to charge at 1 B

$V_1=\frac{q_1}{4\pi {ϵ}_0\left(\frac{d}{2}\right)}+\frac{4}{4\pi {ϵ}_9\left(\frac{d}{2}\right)}=\frac{1}{4\pi {ϵ}_0\left(\frac{d}{2}\right)}(q_1+q_2)$

Where, Eo = Permittivity of free space

$\begin{array}{l}\frac{1}{4\pi {ϵ}_0}=9\times {10}^{9}N{C}^2{m}^{-2}\\ \therefore V_1=\frac{9\times {10}^{\circ }\times {10}^{-6}}{\left(\frac{0.30}{2}\right)}(2.5+1.5)=2.4\times {10}^{5}V\end{array}$

$\begin{array}{l}{\mathrm{E}}_1=\text{ Electric field due to }{\mathrm{q}}_2-\text{ Electric field due to }{\mathrm{q}}_1=\frac{{\mathrm{q}}_2}{4{\mathrm{\pi ϵ}}_0(\frac{\mathrm{d}}{2}{)}^2-\frac{{\mathrm{q}}_1}{4{\mathrm{\pi ϵ}}_0}(\frac{\mathrm{d}}{2}{)}^2}\\ =\frac{9\times {10}^9}{(\frac{0.30}{2}{)}^2\times {10}^6\times (2.5-1.5)}\\ = 4 \times {10}^5 {\mathrm{Vm}}^{-1}\end{array}$

Therefore, the potential at mid-point is 2.4 x 105 V and the electric field at mid-point is 4 x 103 V m. The field is directed from the larger charge to the smaller charge.

(b) Consider a point Z such that normal distance 0Z = 10 cm =0.1 m, as shown in the following figure. V2 and E2 are the electric potentials and electric fields respectively at Z.

It can be observed from the figure that distance,

$BZ=AZ=\sqrt{(0.1{)}^2+(0.15{)}^2}=0.18m$

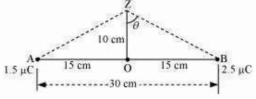
V2 Electric potential due to A + Electric Potential due to B

$\begin{array}{l}=\frac{q_1}{4\pi {ϵ}_0\left(AZ\right)}+\frac{q_1}{4\pi {ϵ}_0\left(BZ\right)}\\ =\frac{9\times {10}^9\times {10}^{-6}}{0.18}(1.5+2.5)\\ =2\times {10}^{5}V\end{array}$

Electric field due to q at Z,

$\begin{array}{l}{E}_A=\frac{q_1}{4\pi {ϵ}_0(AZ{)}^2}\\ =\frac{9\times {10}^{\circ }\times 1.5\times {10}^{-6}}{(0.18{)}^2}\\ =0.416\times {10}^{\circ }V/m\end{array}$

Electric field due to q2 at Z,

$\begin{array}{l}{E}_B=\frac{q_2}{4\pi {ϵ}_0(BZ{)}^2}\\ =\frac{9\times {10}^9\times 2.5\times {10}^{-6}}{(0.18{)}^2}\\ =0.69\times {10}^{6}V{m}^{-1}\end{array}$

The resultant field intensity at Z,

$E=\sqrt{E_A^2+E_B^2+2E_A{E}_B\cos 2\theta }$

Where, 28 is the angle, AZ B

From the figure, we obtain

$\begin{array}{l}\cos \theta =\frac{0.10}{0.18}=\frac{5}{9}=0.5556\\ \theta ={\cos }^{-1}0.5556=56.25\\ \therefore 2\theta ={112.5}^{\circ }\\ \cos 2\theta =-0.38\\ E=\sqrt{(0.416\times {10}^{\circ }{)}^2\times (0.69\times {10}^{\circ }{)}^2+2\times 0.416\times 0.69\times {10}^2\times (-0.38)}\\ =6.6\times {10}^{4}V{m}^{-4}\end{array}$

Therefore, the potential at a point 10 cm (perpendicular to the mid-point) is 2.0 x ${10}^5$V and electric field is $6.6 \mathrm{X} {10}^5 {\mathrm{Vm}}^{-1}.$