Ncert Exercises & Solutions

2.16 (a) Show that the normal component of the electrostatic field has a discontinuity from one side of a charged surface to another given by

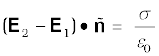
where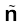is a unit vector normal to the surface at a point and σ is the surface charge density at that point. (The direction of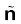is from side 1 to side 2.) Hence, show that just outside a conductor, the electric field is σ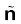/ε0.

(b) Show that the tangential component of the electrostatic field is continuous from one side of a charged surface to another.
[Hint: For (a), use Gauss’s law. For, (b) use the fact that work done by the electrostatic field on a closed loop is zero.]

Electric field on one side or a charged body Is Ei and electric field on the other side of the same body is E2. If infinite plane charged body has a uniform thickness, then electric field due to one surface of the charged body Is given by,

${\bar{E}}_{1} = - \frac{σ}{2 ϵ_{0}} \hat{n} . . . (i)$ ${\bar{E}}_{1} = - \frac{σ}{2 ϵ_{0}} \hat{n} . . . (i)$

Where,

$\hat{n}$ $\hat{n}$ = Unit vector normal to the surface at a point a Surface charge
density at that point.

Electric field due to the other surface of the charged body,

$\vec{E_{2}} = - \frac{σ}{2 ϵ_{0}} \hat{n} . . . (ii)$ $\vec{E_{2}} = - \frac{σ}{2 ϵ_{0}} \hat{n} . . . (ii)$

Electric field at any point due to the two Surfaces,

$\begin{array}{l} \bar{E_{2}} - \bar{E_{1}} = \frac{σ}{2 ϵ_{0}} \hat{n} + \frac{σ}{2 ϵ_{0}} \hat{n} = \frac{σ}{ϵ_{0}} \hat{n} \\ (\vec{E_{2}} - \vec{E_{1}}) \cdot n = \frac{σ}{ϵ_{9}} \end{array}$ $\begin{array}{l} \bar{E_{2}} - \bar{E_{1}} = \frac{σ}{2 ϵ_{0}} \hat{n} + \frac{σ}{2 ϵ_{0}} \hat{n} = \frac{σ}{ϵ_{0}} \hat{n} \\ (\vec{E_{2}} - \vec{E_{1}}) \cdot n = \frac{σ}{ϵ_{9}} \end{array}$

Since inside a closed conductor, $\vec{E} = 0$ $\vec{E} = 0$ ,

$∴ \vec{E} = {\vec{E}}_{2} = - \frac{σ}{2 ϵ_{0}} \hat{n}$ $∴ \vec{E} = {\vec{E}}_{2} = - \frac{σ}{2 ϵ_{0}} \hat{n}$

Therefore, the electric field just outside the conductor is $\frac{σ}{ϵ_{n}} \hat{n}$ $\frac{σ}{ϵ_{n}} \hat{n}$ .

(b) When a charged particle is moved from one point to the other on a closed-loop, the work done by the electrostatic field is zero. Hence, the tangential component of the electrostatic field is continuous from one side of a charged surface to the other.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions