Signup | Login

Question 2.25:

Obtain the equivalent capacitance of the network in Figure. For a 300 V supply, determine the charge and voltage across each capacitor.


 
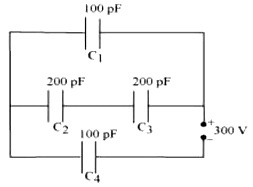
The capacitance of capacitor C1 is 100 PF.
The capacitance Of capacitor C2 is 200 PF.
The capacitance of capacitor C3 is 200 PF.
The capacitance of capacitor C4 is 100 PF.
Supply potential, V = 300 V
Capacitors C2 and C3 are connected in series.
Let their equivalent capacitance be C'. Therefore,
1C′=1200+1200=2200=1100⇒C′=100pF
Capacitors C1 and C2 are in parallel. Let their equivalent capacitance be C".
C" = C' +C = 100 + 100 = 200 pF
C" and C4 are connected in series. Let their equivalent capacitance be C.
1C=1C′′+1C4=1200+1100=3200⇒C=2003pF
Hence, the equivalent capacitance of the circuit is pF
The Potential difference across C" = V"
The potential difference across C4 = V4
∴V′′+V4=V=300 V
Charge on C4 is given by
Q4=CV=2003×10−12×300=2×10−8C∴V4=Q4C4=2×10−8100×10−12=200 V∴ Voltage across C1 is given by, V1=V−V4=300−200=100 V
Hence, the potential difference, V1, across C1 is 100 V.
 
Charge on C1 is given by,
Q1=C1V1=100×10−12×100=10−8C
C2 and C3 have the same capacitances have a potential difference of 100 V together. Since C2 and C3 are in series, the potential difference across C2 and C3 is given by, V2 = V3 = 50 v
Therefore, charge on C2 is given by,
Q2=C2V2=200×10−12×50=10−8C
And charge on C3 is given by,
Q3=C3V3=200×10−12×50=10−8C
Hence, the equivalent capacitance Of the given circuit is 200/3 pF with
 
Q1=10−8C,V1=100 VQ2=10−8C,V2=50 VQ3=10−8C,V3=50 VQ4=2×10−8C,V4=200 V
 

NEET Information

courses

Company


Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions

© 2024 GoodEd Technologies Pvt. Ltd.