Question 2.29:
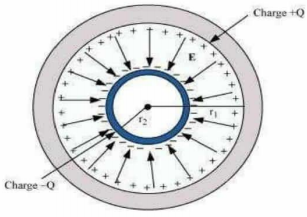
A spherical capacitor consists of two concentric spherical conductors, held in position by suitable insulating supports (Fig. 2.36). Show that the capacitance of a spherical capacitor is given by C = Where r1 and r2 are the radii of outer and inner spheres, respectively.

© 2026 GoodEd Technologies Pvt. Ltd.