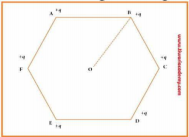
A regular hexagon with sides of length \(10~\text{cm}\) has a charge of \(5~\mu\text C\) at each of its vertices. What is the electric potential at the center of the hexagon? (Assume the potential at infinity is zero.)
1. \(2.7 \times 10^6~\text V\)
2. \(4.5 \times 10^6~\text V\)
3. \(9.0 \times 10^6~\text V\)
4. \(1.8 \times 10^7~\text V\)

© 2026 GoodEd Technologies Pvt. Ltd.