Ncert Exercises & Solutions

Let there be n resistors $R_{1} . . . . . . . . . . R_{2}$ , with $R_{\max} = \max (R_{1} . . . . . . . . . . . . . R_{n})$ and $R_{\min} = \min (R_{1} . . . . . . . . . . . . . R_{n})$ . Show that when they are connected in parallel, the resultant resistance $R_{p} < R_{\min}$ and when they are connected in series, the resultant resistance $R_{s} > R_{\max}$ . Interpret the result physically.

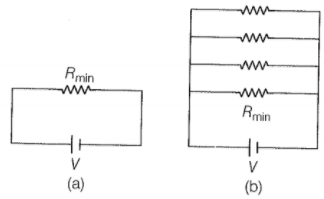
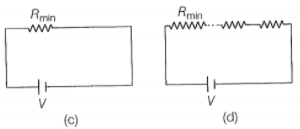
Hint: Use the concept of series and parallel combination of resistors.

Step 1:

When all resistances are connected in parallel, the resultant resistance R is given by;

\frac{1}{R_{p}} = \frac{1}{R_{1}} + \dots \dots . . + \frac{1}{R_{n}}

On multiplying both sides by

R_{\min}

, we have;

\frac{R_{\min}}{R_{p}} = \frac{R_{\min}}{R_{1}} + \frac{R_{\min}}{R_{2}} + \dots . . + \frac{R_{\min}}{R_{n}}

Here, in RHS, there exist one term

\frac{R_{\min}}{R_{\min}}

= 1 and other terms are positive, so we have;

\frac{R_{\min}}{R_{p}} = \frac{R_{\min}}{R_{1}} + \frac{R_{\min}}{R_{2}} + \dots . + \frac{R_{\min}}{R_{n}} > 1

This shows that the resultant resistance

R_{p} < R_{\min}

Thus, in parallel combination, the equivalent resistance of resistors is less than the minimum resistance available in a combination of resistors.

Step 2:

Now, in series combination, the equivalent resistance is given by:

R_{s} = R_{1} + \dots \dots + R_{n}

Here, in RHS, there exist one term having resistance

R_{\max}

So, we have;

\begin{array}{l} R_{s} = R_{1} + \dots + R_{\max} + \dots + R_{n} = R_{\max} + \dots (R_{1} + \dots +) R_{n} \\ or R_{s} \geq R_{\max} \end{array}

Thus, in a series combination, the equivalent resistance of resistors is greater than the maximum resistance available in a combination of resistors.

Physical interpretation:

In fig. (b),

R_{\min}

provides an equivalent route as in Fig. (a) for current. But in addition, there are (n-1) routes by the remaining (n-1) resistors. The current in fig. (b) is greater than the current in Fig. (a). Effective resistance in Fig. (b)<

R_{\min}

. The second circuit evidently affords a smaller resistance.

In Fig. (d),

R_{\max}

provides an equivalent route as in Fig. (c) for current. Current in Fig. (d)< current in Fig. (c). Effective resistance in Fig (d)>

R_{\max}

. The second circuit evidently affords a greater resistance.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions