iii. Equivalent resistance
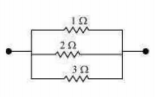
Consider the following combination of the resistors.
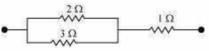
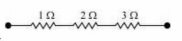
iV. Equivalent resistance
Consider the following combination of the resistors.
Equivalent resistance is given by,
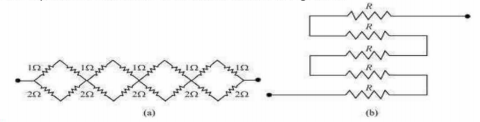
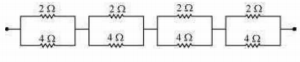
(c) (a) It can be observed from the given circuit that in the first small loop, two resistors of resistance 1 Ω each are connected in series.
Hence, their equivalent resistance = (1+1) = 2 Ω
It can also be observed that two resistors of resistance 2 Ω each are connected in series.
Hence, their equivalent resistance=(2+2)=4 Ω.
Therefore, the circuit can be redrawn as
It can be observed that 2 Ω and 4 Ω resistors are connected in parallel in all the four loops.
Hence, equivalent resistance (R') of each loop is given by,
The circuit reduces to
All the four resistors are connected in series.
Hence, equivalent resistance of the given circuit is
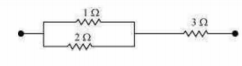
(b) It can be observed from the given circuit that five resistors of resistance R each are connected in series. Hence, equivalent resistance of the circuit=R+R+R+R+R=5R