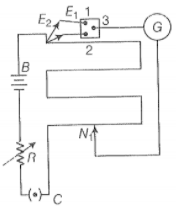
Hint: The potential drop in the potentiometer wire is directly proportional to the length of the wire.
Step 1: Let R' be the resistance of the potentiometer wire.
Effective resistance of potentiometer and a variable resistor (R = 50) is given by = 50 + R'
The effective voltage applied across potentiometer = 10V
The current through the main Circuit,
The potential difference across the wire of potentiometer =
Step 2: Since with a 50 resistor, the null point is not obtained. It is possible only when;
Similarly, with a 10 resistor, a null point is obtained. It's possible only when;
Any R' between 160 and 200 will work.
Step 3: Since the null point is on the last (4th) segment of the potentiometer, therefore potential drop across 400 cm of wire > 8V.
This implies that the potential gradient
kx 400 cm > 8V
kx 4m > 8V
or k>2V/m
Similarly, potential drop across 300 cm wire < 8V
or kx 300cm < 8V
kx 3m < 8V