Ncert Exercises & Solutions

An electron and a positron are released from (0, 0, 0) and (0, 0, 1.5R ) respectively, in a uniform magnetic field B = $B_{0} \hat{i}$ , each with an equal momentum of magnitude p = eBR. Under what conditions on the direction of momentum will the orbits be non-intersecting circles?

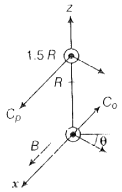
Hint: The distance between the centre of the paths should be more than the radius of paths.

Step 1: Since, B is along the x-axis, for a circular orbit the momenta of the two particles are in the y-z plane. Let

$p_{1} and p_{2}$ be the momentum of the electron and positron, respectively. Both traverse a circle of radius R of the opposite sense. Let

$p_{1}$ make an angle with the y-axis,

$p_{2}$ must make the same angle.

The centers of the respective circles must be perpendicular to the momenta and at a distance R. Let the center of the electron be at

$C_{e}$ and of the position at

$C_{p}$ .

The coordinates of

$C_{e}$ ,

$C_{e} = (0, - Rsinθ, Rcosθ)$

The coordinates of

$C_{p}$ ,

$C_{p} = [0, - Rsinθ, (1.5 R - Rcosθ)]$

The circles of the two shall not overlap if the distance between the two centers is greater than 2R.

Step 2: Let d be the distance between

$C_{p}$ and

$C_{e}$ .

Then,

$\begin{array}{l} d^{2} = (2 Rsinθ)^{2} + {(\frac{3}{2} R - 2 Rcosθ)}^{2} \\ = 4 R^{2} \sin^{2} θ + \frac{9}{4} R^{2} - 6 R^{2} cosθ + 4 R^{2} \cos^{2} θ \\ = 4 R^{2} + \frac{9}{4} R^{2} - 6 R^{2} cosθ \end{array}$

Step 3: Since d has to be greater than 2R;

$d^{2} > 4 R^{2}$

$\Rightarrow 4 R^{2} + \frac{9}{4} R^{2} - 6 R^{2} \cos θ > 4 R^{2}$

$\Rightarrow \frac{9}{4} > 6 \cos θ$

$or \cos θ < \frac{3}{8}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions