Ncert Exercises & Solutions

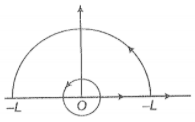
Consider a circular current-carrying loop of radius R in the x-y plane with center at the origin. Consider the line integral $\sum (L) = ∣ ∣ \int_{- L}^{L} B . dl ∣ ∣$ $\sum (L) = |\int_{- L}^{L} B . dl|$ taken along the z-axis.

(a) Show that $\sum$ $\sum$ (L) monotonically increases with L.

(b) Use an appropriate Amperian loop to show that $\sum$ $\sum$ (∞) = $μ_{0} I$ $μ_{0} I$ , where l is the current in the wire.

(d) Suppose we replace the circular coil by a square coil of sides R carrying the same current I. What can you say about $\sum$ $\sum$ (L) and $\sum$ $\sum$ (∞)?

Hint: Apply the ampere-circuital law.

(a) Step 1: B(z) points in the same direction on the z-axis and hence,

\sum

$\sum$ (L) is a monotonically function of L.

Since, B and dl are along the same direction, therefore, B.dl = Bdl as cos0= 1

(b) Step 2:

\sum

$\sum$ (L) + contribution from large distance on contour

C = μ_{0} l

$C = μ_{0} l$

$∴ as L \to \infty$
Contribution from a large distance

$\to 0 (as B \propto 1 / r^{3})$

$\sum (\infty) = μ_{0} I$
(c) Step 3: The magnetic field due to circular current-carrying loop of radius R in the x-y plane with center at original any point lying at a distance L from the origin,

$B_{z} = \frac{μ_{0} {IR}^{2}}{2 (z^{2} + R^{2})^{3 / 2}}$

$\int_{- \infty}^{\infty} B . dz = \int_{- \infty}^{\infty} \frac{μ_{0} {IR}^{2}}{2 (z^{2} + R^{2})^{3 / 2}} dz$

$Put, z = {Rtanθ}_{1}$

$\Rightarrow dz = {Rsec}^{2} θdθ$

$∴ \int_{- \infty}^{\infty} B_{z} dz = \frac{μ_{0} I}{2} \int_{- π / 2}^{π / 2} cosθdθ = μ_{0} I$

(d) Step 4:

$\begin{array}{l} B (Z)_{square} < B (Z)_{circular coil} \\ ∴ \sum (L)_{square} < \sum (L)_{circular coil} \\ But by using arguments as in (b), \\ \sum (\infty)_{square} = \sum (\infty)_{circular} \end{array}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions