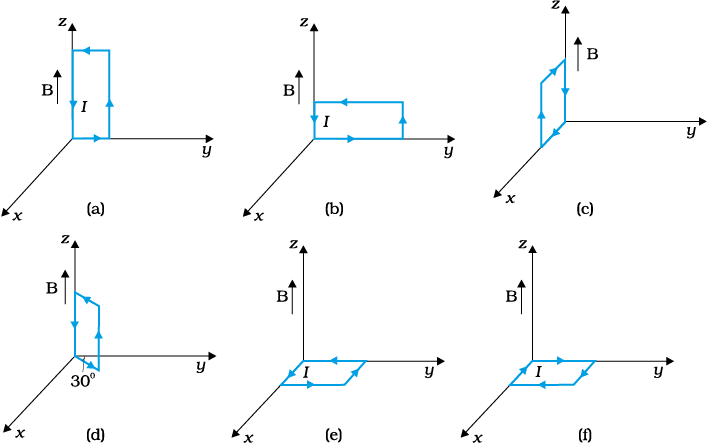
Magnetic field strength, B = 3000 G = 3000 × 10-4 T = 0.3 T
Length of the rectangular loop, l = 10 cm
Width of the rectangular loop, b = 5 cm
Area of the loop, A = l × b = 10 × 5 = 50 cm2 = 50 × 10-4 m2
Current in the loop, I = 12 A
Now, taking the anti-clockwise direction of the current as positive and vice-versa:
(a) Torque, →τ=I→A×→B
From the given figure, it can be observed that A is normal to the y-z plane and B is directed along the z-axis.
∴τ=12×(50×10-4)ˆi×0.3ˆk
=-1.8×10-2 ˆj N m
The torque is 1.8 × 10-2 N m along the negative y-direction. The force on the loop is zero because the angle between A and B is zero.
(b) This case is similar to case (a). Hence, the answer is the same as (a).
(c) Torque τ=I→A×→B
From the given figure, it can be observed that A is normal to the x-z plane and B is directed along the z-axis.
∴τ=-12×(50×10-4)ˆj×0.3ˆk
=-1.8×10-2ˆi N m
The torque is 1.8 × 10-2 N m along the negative x direction and the force is zero.
(d) Magnitude of torque is given as:
|τ|=IAB
=12×50×10-4×0.3
=1.8×10-2 N m
The torque is 1.8 × 10-2 N m at an angle of 240° with positive x direction. The force is zero.
(e) Torque τ=I→A×→B
=(50×10-4×12)ˆk×0.3ˆk
=0
Hence, the torque is zero. The force is also zero.
(f) Torque τ=I→A×→B
=(50×10-4×12)ˆk×0.3ˆk
=0
Hence, the torque is zero. The force is also zero.
In case (e), the direction of I→A and →B is the same and the angle between them is zero. If displaced, the come back to an equilibrium. Hence, its equilibrium is stable.
Whereas, in case (f), the direction of I→A and →B is opposite. The angle between them is 180°. If disturbed, it does not come back to its original position. Hence, its equilibrium is unstable.
