Ncert Exercises & Solutions

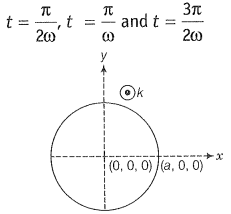
A magnetic field in a certain region is given by $B = B_{0} \cos (ω t) \hat{k}$ and a coil of radius a with resistance R is placed in the x-y plane with its centre at the origin in the magnetic field (figure). Find the magnitude and the direction of the current at (a, 0, 0) at

Hint: The current in the coil depends on the rate of change of magnetic flux.

Step 1: At any instant, flux passes through the ring is given by;

$ϕ = B . A = BAcosθ = BA (∵ θ = 0)$

$or ϕ = B_{0} ({πa}^{2}) \cos ωt$

By Faraday's law of electromagnetic induction,

The magnitude of induced emf is given by;

$ε = |- \frac{dϕ}{dt}| = B_{0} ({πa}^{2}) ωsinωt$

This causes the flow of induced current, which is given by;

$I = B_{0} ({πa}^{2}) ωsinωt / R$

Step 2: Now, finding the value of current at different instants, so we have current at:

$t = \frac{π}{2 ω}$

$I = \frac{B_{0} ({πa}^{2}) ω}{R}$ along

$\hat{j}$

Because

$sinωt = \sin (ω \times \frac{π}{2 ω}) = \sin \frac{π}{2} = 1$

$At t = \frac{π}{ω}, I = \frac{B ({πa}^{2}) ω}{R} sinπ = 0$

Here,

$sinωt = \sin (ω \times \frac{π}{ω}) = sinπ = 0$

$t = \frac{3}{2} \frac{π}{ω}$

$I = \frac{B ({πa}^{2}) ω}{R} along - \hat{j}$

$sinωt = \sin (ω \times \frac{3 π}{2 ω}) = \sin \frac{3 π}{2} = - 1$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions