Ncert Exercises & Solutions

In the L-C-R circuit, shown in the figure the AC driving voltage is $V = V_{m} sin ωt$ $V = V_{m} \sin ωt$ .

(a) Write down the equation of motion for q(t).

(b) At $t = t_{0}$ $t = t_{0}$ , the voltage source stops and R is short-circuited. Now write down how much energy is stored in each of L and C.

Hint: Use Kirchoff's law.

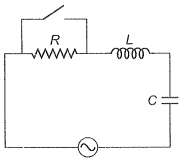
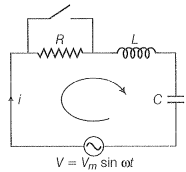
Step 1: (a) Consider the R-L-C circuit shown in the adjacent diagram.

Given,

V = V_{m} sin ωt

$V = V_{m} \sin ωt$

Let current at any instant be i.

Applying KVL in the given circuit;

i R + L \frac{d i}{d t} + \frac{q}{C} - V_{m} sin ω t = 0 . . . (i)

$i R + L \frac{d i}{d t} + \frac{q}{C} - V_{m} \sin ω t = 0 . . . (i)$

Now, we can write,

i = \frac{d q}{d t} \Rightarrow \frac{d i}{d t} = \frac{d^{2} q}{d t^{2}}

$i = \frac{d q}{d t} \Rightarrow \frac{d i}{d t} = \frac{d^{2} q}{d t^{2}}$

From Eq. (i),

\frac{d q}{d t} R + L \frac{d^{2} q}{d t^{2}} + \frac{q}{C} = V_{m} sin ω t

$\frac{d q}{d t} R + L \frac{d^{2} q}{d t^{2}} + \frac{q}{C} = V_{m} \sin ω t$

\Rightarrow L \frac{d^{2} q}{d t^{2}} + R \frac{d q}{d t} + \frac{q}{C} = V_{m} sin ω t

$\Rightarrow L \frac{d^{2} q}{d t^{2}} + R \frac{d q}{d t} + \frac{q}{C} = V_{m} \sin ω t$

This is the required equation of variation (motion) of charge.

(b) Step 2:

L e t q = q_{m} sin (ω t + ϕ) = - q_{m} cos (ω t + ϕ)

$L e t q = q_{m} \sin (ω t + ϕ) = - q_{m} \cos (ω t + ϕ)$

i = i_{m} sin (ω t + ϕ) = q_{m} ω sin (ω t + ϕ)

$i = i_{m} \sin (ω t + ϕ) = q_{m} ω \sin (ω t + ϕ)$

i_{m} = \frac{V_{m}}{Z} = \frac{V_{m}}{\sqrt{R^{2} + {(X_{C} - X_{L})}^{2}}}

$i_{m} = \frac{V_{m}}{Z} = \frac{V_{m}}{\sqrt{R^{2} + {(X_{C} - X_{L})}^{2}}}$

ϕ = {tan}^{- 1} (\frac{X_{C} - X_{L}}{R})

$ϕ = \tan^{- 1} (\frac{X_{C} - X_{L}}{R})$

Step 3: When R is short-circuited at

t = t_{0}

$t = t_{0}$ , the energy is stored in L and C.

U_{L} = \frac{1}{2} {Li}^{2} = \frac{1}{2} L {[\frac{V_{m}}{\sqrt{{(R^{2} + X_{C} - X_{L})}^{2}}}]}^{2} {sin}^{2} ({ωt}_{0} + ϕ)

$U_{L} = \frac{1}{2} {Li}^{2} = \frac{1}{2} L {[\frac{V_{m}}{\sqrt{{(R^{2} + X_{C} - X_{L})}^{2}}}]}^{2} \sin^{2} ({ωt}_{0} + ϕ)$

and U_{C} = \frac{1}{2} \times \frac{q^{2}}{C} = \frac{1}{2 C} [q^{2} m {cos}^{2} ({ωt}_{0} + ϕ)]

$and U_{C} = \frac{1}{2} \times \frac{q^{2}}{C} = \frac{1}{2 C} [q^{2} m \cos^{2} ({ωt}_{0} + ϕ)]$

$= \frac{1}{2 C} \times {(\frac{i_{m}}{ω})}^{2} \cos^{2} ({ωt}_{0} + φ) [∵ i_{m} = q_{m} ω]$

$= \frac{1}{2 C} {[\frac{V_{m}}{\sqrt{R^{2} + {(X_{C} - X_{L})}^{2}}}]}^{2} \frac{\cos^{2} ({ωt}_{0} + ϕ)}{ω^{2}}$

$= \frac{1}{2 {Cω}^{2}} {[\frac{V_{m}}{\sqrt{R^{2} + {(X_{C} - X_{L})}^{2}}}]}^{2} \cos^{2} ({ωt}_{0} + ϕ)$

(c) Step 4: When R is short-circuited, the circuit becomes an L-C oscillator. The capacitor will go on discharging and all energy will go to L and back and forth. Hene, there is an oscillation of energy from electrostatic to magnetic and magnetic to electrostatic.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions