Consider a ray of light incident from the air onto a slab of glass (refractive index \(n\)) of width \(d\), at an angle \(\theta\). The phase difference between the ray reflected by the top surface of the glass and the bottom surface is:
1. \(\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^2} \sin ^2 \theta\right)^{1 / 2}+\pi\)
2. \(\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^2} \sin ^2 \theta\right)^{1 / 2}\)
3. \(\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^2} \sin ^2 \theta\right)^{1 / 2}+\frac{\pi}{2}\)
4. \(\frac{4 \pi d}{\lambda}\left(1-\frac{1}{n^2} \sin ^2 \theta\right)^{1 / 2}+2\pi\)
(a) Hint: The ray reflected by the bottom surface covers an extra path inside the slab.
Step 1: Find the time taken by the ray to move into the slab.
Consider the diagram, the ray (P) is incident at an angle and gets reflected in the direction P' and refracted in the direction P". Due to reflection from the glass medium, there is a phase change of .
Time taken to travel along OP''
From Snell's law,
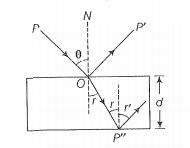
Step 2: Find the phase difference.
Phase difference =

© 2026 GoodEd Technologies Pvt. Ltd.