The optical properties of a medium are governed by the relative permittivity () and relative permeability () . The refractive index is defined as . For ordinary material, and the positive sign is taken for the square root.
In 1964, a Russian scientist V. Veselago postulated the existence of
material with <0 and <0. Since then such metamaterials have
been produced in the laboratories and their optical properties studied.
For such materials . As light enters a medium of such
refractive index the phases travel away from the direction of
propagation.
(i) According to the description above show that if rays of light enter
such a medium from air (refractive index = 1) at an angle in 2nd
quadrant, then the refracted beam is in the 3rd quadrant.
(ii) Prove that Snell's law holds for such a medium.
Hint: The refraction of the light depends on the refractive index of the medium.
Step 1: Find the deviation of a light ray when it enters into such a medium.
Let assume that the given postulate is true, then two parallel rays would proceed as shown in the figure below.
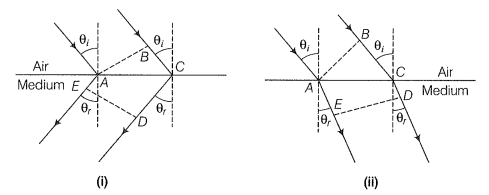
(i) Let AB represent the incident wavefront and DE represents the refracted wavefront. All points on a wavefront must be in the same phase and in turn, must have the same optical path length,
As showing that the postulate is reasonable. If however, the light proceeded in the same it does for ordinary material ( viz. in the fourth quadrat, Fig. 2);
which is obvious from Fig (i).
Hence, the postulate is reasonable.
However, if the light proceeded in the sense it does for ordinary material, (going from 2nd quadrant to 4th quadrant) as shown in Fig. (i), then proceeding as above,
As AE > CD, therefore BC < 0 which is not possible. Hence, the given postulate is correct.
Step 2: Find if the theory proves Snell's law.
(ii) From fig. (i);
which proves Snell's law.

© 2026 GoodEd Technologies Pvt. Ltd.