To ensure almost 100% transmissivity, photographic lenses are often coated with a thin layer of dielectric material. The refractive index of this material is intermediated between that of air and glass (which makes the optical element of the lens). A typically used dielectric film is (n = 1.38). What should the thickness of the film be so that at the centre of the visible spectrum (5500 ), there is a maximum transmission.
Hint: Use Snell's law.
Step 1: Find the optical path difference.
In this figure, we have shown a dielectric film of thickness d deposited on a glass lens.
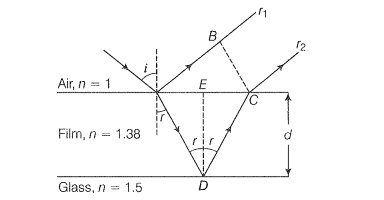
Refractive index of film = 1.38 and refractive index of glass = 1.5
Given,
Consider a ray incident at an angle i. A part of this ray is reflected from the air-film interface and a part is refracted inside. This is partly reflected at the film-glass interface and a part transmitted. A part of the reflected ray is reflected at the film-air interface and a part transmitted as parallel to . Of course, successive reflections and transmissions will keep on decreasing the amplitude of the wave.
Hence, rays and r shall dominate the behaviour. If the incident light is to be transmitted through the lens, and should interfere destructively. Both the reflections at A and D are from lower to higher refractive index and hence, there is no phase change on reflection. The optical path difference between and is n(AD+CD)-AB.
lf d is the thickness of the film, then;
Hence, AB=.
Step 2: Find the conditions for maxima and minima.
For these waves to interfere destructively path difference
For photographic lenses, the sources are normally in the vertical plane,

© 2026 GoodEd Technologies Pvt. Ltd.