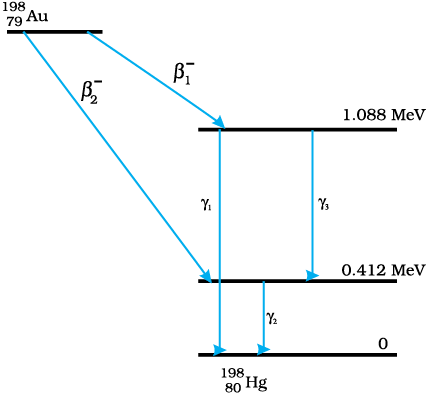
Hint: The maximum kinetic energy of β-particles is the maximum difference in the energy levels.
Step 1: Find the radiation frequencies of γ1-decay.
It can be observed from the given y-decay diagram that γ1-decay from the 1.088 MeV
energy level to the 0 MeV energy level.
Hence, the energy corresponding to γ1-decay is given as:
\(E_{1}=1.088-0=1.088 \quad \mathrm{MeV}\\ h \nu_{1}=1.088 \times 1.6 \times 10^{-19} \times 10^{6} \quad \mathrm{~J}\\ where, h= Planck's~constan t=6.6 \times 10^{-34} J s\\ \nu_{1}= \text{Frequency of radiation radiated by} ~\gamma_{1}-decay\\ \therefore \nu_{1}=\frac{E_{1}}{h}=\frac{1.088 \times 1.6 \times 10^{-19} \times 10^{6}}{6.6 \times 10^{-34}}=2.637 \times 10^{20} \mathrm{~Hz} \)
Step 2: Find the radiation frequencies of γ2-decay.
It can be observed from the given y-decay diagram that decays from the 0.412 MeY energy level to the 0 MeV energy level.
Hence, the energy corresponding to -decay is given as:
\(E_{2}=0.412-0=0.412 \quad \mathrm{MeV}\\ h \nu_{2}=0.412 \times 1.6 \times 10^{-19} \times 10^{6} \mathrm{~J}\\ where, \nu_{2}= \text{Frequency of radiation radiated by}~\gamma_{2}-decay\\ \therefore \nu_{2}=\frac{E_{2}}{h}=\frac{0.412 \times 1.6 \times 10^{-19} \times 10^{6}}{6.6 \times 10^{-34}}=9.988 \times 10^{19} \mathrm{~Hz}\)
Step 3: Find the radiation frequencies of γ3-decay.
It can be observed from the given y-decay diagram that decays from the 1.088 MeV energy level to the 0.412 MeV energy level.
Hence, the energy corresponding to -decay is given as:
\(E_{3}=1.088-0.412=0.676 \mathrm{MeV}\\ h\nu_{3}=0.676 \times 10^{-19} \times 10^{6} J\\ where, v_{3}=\text{ Frequency of radiation radiated by}~\gamma_{3}-decay\\ \therefore \nu_{3}=\frac{E_{3}}{h}=\frac{0.676 \times 1.6 \times 10^{-19} \times 10^{6}}{6.6 \times 10^{-34}}=1.639 \times 10^{20} \quad \mathrm{Hz}\)
Step 4: Find the maximum kinetic energy of β--particles.