1.29 A hollow charged conductor has a tiny hole cut into its surface. Show that the electric field in the hole is (, where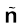 is the unit vector in the outward normal direction, and σ is the surface charge density near the hole.
is the unit vector in the outward normal direction, and σ is the surface charge density near the hole.
Let us consider a conductor with a cavity or a hole. Electric field inside the cavity is zero.
Let E is the electric field just outside the conductor, q is the electric charge, a is the charge density and is the permittivity of free space.
Charge q = X ds
According to Gauss's law, flux,
Therefore, the electric field just outside the conductor is . This field is a superposition of field due to the cavity E and the field due to the rest of the charged conductor E. These fields are equal and opposite inside the conductor and equal in magnitude and direction outside the conductor.
Hence, the field due to the rest of the conductor is .

© 2026 GoodEd Technologies Pvt. Ltd.