1.30 Obtain the formula for the electric field due to a long thin wire of uniform linear charge density E without using Gauss’s law. [Hint: Use Coulomb’s law directly and evaluate the necessary integral.]
Take a long thin wire XY (as shown in the following figure) of uniform linear charge density

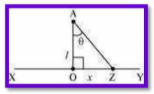
Consider a point A at a perpendicular distance I from the mid-point
O of the wire, as shown in the following figure.
Let E be the electric field at point A due to the wire, XY.
Consider a small length element dx on the wire section with OZ X
Let q be the charge on this piece.
The electric field is resolved into two rectangular components. dE cos is the perpendicular component and dE sin G is the parallel component. When the whole wire is considered, the component dE sin G is cancelled. Only the perpendicular component dEcos6 affects point A.
Hence, effective electric field at point A due to the element dx is dEj.
On differentiating equation (2), we obtain
From equation (2), we have
Putting equations (3) and (4) in equation (1), we obtain
The wire is so long that 6 tends from
By integrating equation (5), we obtain the value of field E as,
Therefore, the electric field due to long wire is .

© 2026 GoodEd Technologies Pvt. Ltd.