Ncert Exercises & Solutions

14.11 Figures 14.25 correspond to two circular motions. The radius of the circle, the period of revolution, the initial position, and the sense of revolution (i.e. clockwise or anti-clockwise) are indicated on each figure.

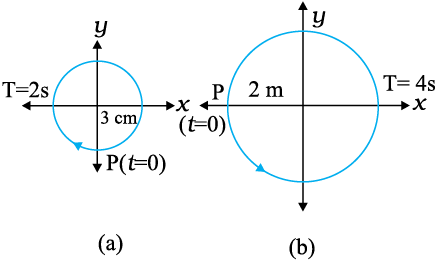
Fig. 14.25

Obtain the corresponding simple harmonic motions of the x-projection of the radius vector of the revolving particle P, in each case.

As we can see in figure (a):

$Time period, T = 2 s$

$Amplitude, A = 3 cm$

$At time t = 0, phase angle φ = + \frac{π}{2}$

$Therefore, the displacement equation for the x - projection of OP, at time t :$

$\begin{array}{l} x = A \cos [\frac{2 π t}{T} + ϕ] \\ = 3 \cos (\frac{2 π t}{2} + \frac{π}{2}) = - 3 \sin (\frac{2 π t}{2}) \\ ∴ x = - 3 \sin π t cm \end{array}$

$For figure (b) :$

$Time period, T = 4 s$

$Amplitude, a = 2 m$

$At time t = 0, phase angle, Φ = + π$

$Therefore, the displacement equation for the x - projection of OP, at time t :$

$x = Acos (\frac{2 πt}{T} + ϕ) = 2 \cos (\frac{2 πt}{4} + π)$

$∴ x = - 2 \cos (\frac{π}{2} t) m$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions