14.20 An air chamber of volume V has a neck area of cross-section 'a' into which a ball of mass 'm' just fits and can move up and down without any friction (Fig.14.27). Show that when the ball is pressed down a little and released, it executes SHM. Obtain an expression for the time period of oscillations assuming pressure-volume variations of air to be isothermal [see Fig. 14.27].
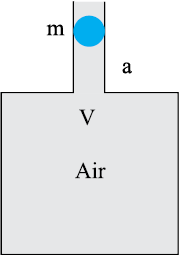
Fig. 14.27
The volume of the air chamber = V
Area of the cross-section of the neck = a
Mass of the ball = m
The pressure inside the chamber is equal to the atmospheric pressure.
Let the ball be depressed by x units. As a result of this depression, there would be a decrease in the volume and an increase in the pressure inside the chamber.
The decrease in the volume of the air chamber, ΔV = ax
Volumetric strain =

© 2026 GoodEd Technologies Pvt. Ltd.