Ncert Exercises & Solutions

Draw a graph to show the variation of PE, KE and total energy of a simple harmonic oscillator with displacement.

Hint: Apply the formulae of PE and KE in SHM.

Step 1: Find the potential energy of SHM.

The potential energy (PE) of a simple harmonic oscillator is

= \frac{1}{2} k x^{2} = \frac{1}{2} m ω^{2} x^{2} . . . (i)

$= \frac{1}{2} k x^{2} = \frac{1}{2} m ω^{2} x^{2} . . . (i)$

Where k=force constant

= m ω^{2}

$= m ω^{2}$

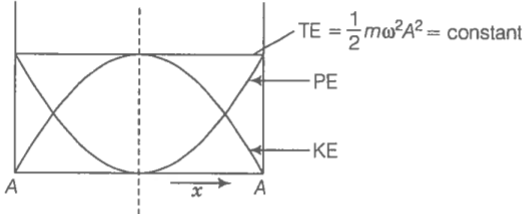
When PE is plotted against displacement x, we will obtain a parabola.

When x =0, PE =0

When

x = \pm A, P E

$x = \pm A, P E$ = maximum

= \frac{1}{2} m ω^{2} A^{2}

$= \frac{1}{2} m ω^{2} A^{2}$

Step 2: Find the KE of SHM.

KE of a simple harmonic oscillator=

\frac{1}{2} m v^{2} [∵ v = ω \sqrt{A^{2} - x^{2}}]

$\frac{1}{2} m v^{2} [∵ v = ω \sqrt{A^{2} - x^{2}}]$

= \frac{1}{2} m {[ω \sqrt{A^{2} - x^{2}}]}^{2}

$= \frac{1}{2} m {[ω \sqrt{A^{2} - x^{2}}]}^{2}$

= \frac{1}{2} m ω^{2} (A^{2} - x^{2}) . . . (i i)

$= \frac{1}{2} m ω^{2} (A^{2} - x^{2}) . . . (i i)$

This is also a parabola if plot KE against displacement x.

i.e.,

K E = 0 a t x = \pm A

$K E = 0 a t x = \pm A$

and

K E = \frac{1}{2} m ω^{2} A^{2} a t x = 0

$K E = \frac{1}{2} m ω^{2} A^{2} a t x = 0$

Step 3: Find the total energy of SHM.

Now, the total energy of the simple harmonic oscillator = PE+KE [using Eqs. (I) and (ii)]

= \frac{1}{2} m ω^{2} x^{2} + \frac{1}{2} m ω^{2} (A^{2} - x^{2})

$= \frac{1}{2} m ω^{2} x^{2} + \frac{1}{2} m ω^{2} (A^{2} - x^{2})$

= \frac{1}{2} m ω^{2} x^{2} + \frac{1}{2} m ω^{2} A^{2} - \frac{1}{2} m ω^{2} x^{2}

$= \frac{1}{2} m ω^{2} x^{2} + \frac{1}{2} m ω^{2} A^{2} - \frac{1}{2} m ω^{2} x^{2}$

T E = \frac{1}{2} m ω^{2} A^{2}

$T E = \frac{1}{2} m ω^{2} A^{2}$

Which is constant and does not depend on x.

Plotting under the above guidelines KE, PE and TE versus displacement x-graph as follows: