Ncert Exercises & Solutions

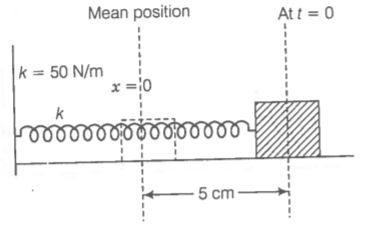
A mass of 2 kg is attached to the spring of the spring constant $50 N / m$ . The block is pulled to a distance of 5 cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.

Hint: The oscillation of the block starts from the extreme position.

Step 1: Find the amplitude and angular frequency of the block.

Consider the diagram of the spring block system. It is an SHM with an amplitude of 5 cm about the mean position shown.

Given, spring constant, k=50 N/m

m = mass attached =2 kg

$∴$ Angular frequency,

$ω = \sqrt{\frac{k}{m}} = \sqrt{\frac{50}{2}} = \sqrt{25} = 5$ rad/s

Step 2: Find the equation of motion of oscillations.

Assuming the displacement function,

y(t)=Asin

$(ω t + ϕ)$

where,

$ϕ$ =initial phase

But given at t=0, y(t) =+A

y(0)=+A=Asin(

$ω \times 0 + ϕ$ )

or sin

$ϕ = 1 \Rightarrow ϕ = \frac{π}{2}$

$∴$ The desired equation is y(t)=Asin

$(ω t + \frac{π}{2}) = A \cos ω t$

Putting A=5 cm,

$ω$ =5 rad/s

we get, y(t)=5sin5t

where, t is in second and y is in centimetre.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions