Ncert Exercises & Solutions

Consider a pair of identical pendulums which oscillate with equal amplitude independently such that when one pendulum is at its extreme position making an angle of 2 $°$ to the right with the vertical, the other pendulum makes an angle of 1 $°$ to the left of the vertical. What is the phase difference between the pendulums?

Hint: The phase difference depends on the positions and direction of motion of the pendulums.

Step 1: Write the equations of SHM for two pendulums.

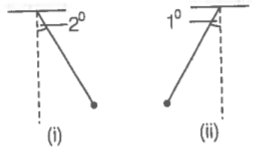
Consider the situations shown in the diagram (i) and (ii).

Assuming the two pendulums follow the following functions of their angular displacements,

$θ_{1} = θ_{0} \sin (ω t + ϕ_{1})$ ...(i)

and

$θ_{2} = θ_{0} \sin (ω t + ϕ_{2})$ ...(ii)

As it is given that amplitude and time period being equal but phases being different.

Step 2: Find the phase of two SHMs.

Now, for the first pendulum at any time t,

$θ_{1} = + θ_{0}$ [Right extreme]

From Eq. (i), we get,

$\Rightarrow θ_{0} = θ_{0} \sin (ω t + ϕ_{1}) o r 1 = \sin (ω t + ϕ_{1})$

$\Rightarrow \sin \frac{π}{2} = \sin (ω t + ϕ_{1})$

$(ω t + ϕ_{1}) = \frac{π}{2}$ ...(iii)

Similarly, at the same instant t for the second pendulum, we have,

$θ_{2} = - \frac{θ_{0}}{2}$

where

$θ_{0} = 2 °$ is the angular amplitude of the first pendulum. For the second pendulum, the angular displacement is one degree, therefore,

$θ_{2} = \frac{θ_{0}}{2}$ and a negative sign is taken to show for being left to the mean position.

From Eq.(ii), then,

$- \frac{θ_{0}}{2} = θ_{0} \sin (ω t + ϕ_{2})$

$\Rightarrow \sin (ω t + ϕ_{2}) = - \frac{1}{2}$

$(ω t + ϕ_{2}) = - \frac{π}{6} o r \frac{7 π}{6}$ ...(iv)

Step 3: Find the phase difference.

From Eqs. (iv) and (iii), the difference in phases,

$(ω t + ϕ_{2}) - (ω t + ϕ_{1}) = \frac{7 π}{6} - \frac{π}{2} = \frac{7 π - 3 π}{6} = \frac{4 π}{6}$

$(ϕ_{2} - ϕ_{1}) = \frac{4 π}{6} = \frac{2 π}{3} = 120 °$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions