Ncert Exercises & Solutions

A box of 1.00 $m^{3}$ $m^{3}$ is filled with nitrogen at 1.50 atm at 300 K. The box has a hole of an area of 0.010 m $m^{2}$ . How much time is required for the pressure to reduce to 0.10 atm, if the pressure outside is 1 atm?

Hint: The total no. of molecules will be equal to the difference of molecules going outside and coming inside.

Step 1: Find the no. of molecules colliding the wall in time interval

$∆$ t.

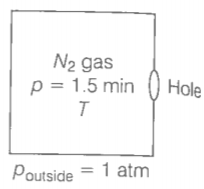
Given, the volume of the box, V=1.00

$m^{3}$

$A r e a = a = 0.010 m m^{2}$

$= 8.01 \times 10^{- 6} m^{2}$

$= 10^{- 8} m^{2}$

Temperature outside = Temperature inside
Initial pressure inside the box = 1.50 atm.
Final pressure inside the box = 0.10 atm.
Assuming,

$v_{i x}$ = Speed of nitrogen molecule inside the box along the x-direction.

$n_{i}$ = number of molecules per unit volume colliding the wall in a time interval of

$∆$ t

All the particles at a distance

$(v_{i x} ∆ t)$ will collide with the hole and the wall, the particle colliding along the hole will escape out reducing the pressure in the box.

Let area of the wall = A

The number of particles colliding in time

$∆ t = \frac{1}{2} n_{i} (v_{i x} ∆ t)$ A

$\frac{1}{2}$ is the factor because all the particles along x-direction are behaving randomly. Hence, half of these are colliding against the walls on either side.

Inside the box,

$v_{i x}^{2} + v_{i y}^{2} + v_{i z}^{2} = v_{r m s}^{2}$

$∴ v_{i x}^{2} = \frac{v_{r m s}^{2}}{3} (∵ v_{i x} = v_{i y} = v_{i z})$

$\frac{1}{2} m v_{r m s}^{2} = \frac{3}{2} k_{B} T$

$[v_{r m s} = R o o t m e a n s q u a r e v e l o c i t y]$

$K_{B} = B o l t z m a n n c o n s \tan t$

$T = T e m p e r a t u r e$

$\Rightarrow v_{r m s}^{2} = \frac{3 k_{B} T}{m}$

$\Rightarrow v_{r m s} = \sqrt{\frac{3 k_{B} T}{m}}$

[According to the kinetic theory of gases]

Now,

$v_{i x}^{2} = \frac{v_{r m s}^{2}}{3} = \frac{1}{3} \times \frac{3 k_{B} T}{m}$

$v_{i x}^{2} = \frac{k_{B} T}{m}$

$∴$ Number of particles colliding in time

$∆ t = \frac{1}{2} n_{i} \sqrt{\frac{k_{B} T}{m}} ∆ t A$

Step 2: Find the difference of molecules going outside and coming inside.

If particles collide along the hole, they move out. Similarly, outside particles colliding along the hole will move inside.

If a = area of hole

Then, net particle flow in time

$∆ t = \frac{1}{2} (n_{i} - n_{o}) \sqrt{\frac{k_{B} T}{m}} ∆ t a$

[Temperatures inside and outside the box are equal]

$p V = μ R T \Rightarrow μ = \frac{p V}{R T}$

Let n= number density of nitrogen

$= \frac{μ N_{A}}{V} = \frac{p N_{A}}{R T} [∵ \frac{μ}{V} = \frac{p}{R T}]$

Let

$N_{A}$ = Avogardro's number

If after time t, the pressure inside changes from p to

$p'$ ;

$∴ n_{i} = \frac{p N_{A}}{R T}$

Step 3: Find the after which the pressure reduces to the final pressure.

Now, number of molecules gone out

$= n_{i} V - n_{o} V$

$= \frac{1}{2} (n_{i} - n_{o}) \sqrt{\frac{k_{B} T}{m}} ta$

$∴ \frac{{pN}_{A}}{RT} V - \frac{p' N_{A}}{RT} V = \frac{1}{2} (p_{1} - p_{2}) \frac{N_{A}}{RT} \sqrt{\frac{k_{B} T}{m}} ta$

$or \frac{{pN}_{A}}{RT} V - \frac{p' N_{A}}{RT} V = \frac{1}{2} (p_{1} - p_{2}) \frac{N_{A}}{RT} \sqrt{\frac{k_{B} T}{m}} ta$

$∴ t = 2 (\frac{p - p'}{p_{1} - p_{2}}) \frac{V}{a} \sqrt{\frac{m}{k_{B} T}}$

Putting the values from the data given,

$t = 2 (\frac{1.5 - 1.4}{1.5 - 1.0}) \frac{1 \times 1.00}{0.01 \times 10^{- 6}} \sqrt{\frac{46.7 \times 10^{- 27}}{1.38 \times 10^{- 23} \times 300}}$

$= 2 (\frac{0.1}{0.5}) \frac{1}{10^{- 8}} \sqrt{\frac{4.7}{1 . 38 \times 3} \times 10^{- 6}}$

$= 2 (\frac{1}{5}) 1 \times 10^{8} \times 10^{- 3} \times \sqrt{\frac{46.7}{4.14}} = \frac{2}{5} \times 10^{5} \sqrt{\frac{45.7}{4.14}}$

$= \frac{2}{5} \times 10^{5} \sqrt{11.28}$

$= \frac{2}{5} \times 3.358 \times 10^{5} = \frac{6.717}{5} \times 10^{5} = 1.343 \times 10^{5} s$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions