Ncert Exercises & Solutions

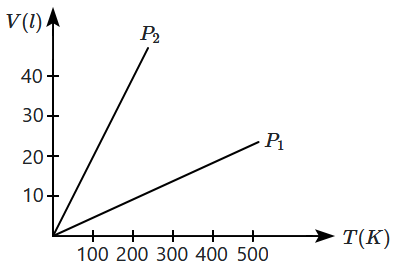
The volume versus temperature graphs for a given mass of an ideal gas are shown in the figure at two different values of constant pressure. What can be inferred about relation between $\mathrm{P_1}$ and $\mathrm{P_2}$ ?

1. $\mathrm{P_1}>\mathrm{P_2}$
2. $\mathrm{P_1}=\mathrm{P_2}$
3. $\mathrm{P_1}<\mathrm{P_2}$
4. data is insufficient

Hint: The slope of the V-T graph gives the pressure.

Step 1: Find the slope of the two graphs.

We know for an ideal gas,

p V = n R T \Rightarrow V = (\frac{n R}{P}) T

$p V = n R T \Rightarrow V = (\frac{n R}{P}) T$

Slope of the V— T graph,

m = \frac{d V}{d T} = \frac{n R}{P}

$m = \frac{d V}{d T} = \frac{n R}{P}$ [m = slope of V-T graph]

\Rightarrow m \propto \frac{1}{P}

$\Rightarrow m \propto \frac{1}{P}$ [

$∴$ nR = constant]

$\Rightarrow P \propto \frac{1}{m}$

Step 2: Find the relation between two pressures.

hence,

$\frac{P_{1}}{P_{2}} = \frac{m_{2}}{m_{1}} < 1 [P = p r e s s u r e]$

where

$m_{1}$ is the slope of the graph corresponding to

$P_{1}$ and similarly

$m_{2}$ is the slope corresponding to

$P_{2}$ .

$\Rightarrow$

$P_{1} > P_{2}$
Hence, option (1) is the correct answer.

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions