Ncert Exercises & Solutions

Consider a rectangular block of wood moving with a velocity $v_{0}$ in gas at temperature T and mass density $ρ$ . Assume the velocity is along the x-axis and the area of cross-section of the block perpendicular to $v_{0}$ is A. Show that the drag force on the block is $4 ρ A_{V_{0}} \sqrt{\frac{k T}{m}}$ , where m is the mass of the gas molecule.

Hint: The drag force will be equal to the rate of momentum transferred by the gas molecules.

Step 1: Find the momentum transferred by the gas molecules.

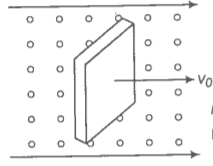
Consider the diagram.

m= mass of the gas

ρ

= density of the gas

Let n = number of molecules per unit volume

v_{r m s}

= RMS speed of the gas molecules

When the block is moving with speed

v_{0}

, the relative speed of molecules w.r.t. front face = v+

v_{0}

coming head-on

The momentum transferred to the block per collision =2m(v+

v_{0}

)

where m=mass of the molecule.

The number of collision in time

∆ t = \frac{1}{2} (v + v_{0}) n ∆ t A

where A = area of cross-section of block and factor of 1/2 appears due to particles moving towards the block.

∴

the momentum transferred in time

∆ t = m {(v + v_{0})}^{2} n A ∆ t

from the front surface.

Similarly, momentum transferred in time

∆ t = m {(v - v_{0})}^{2} n A ∆ t

(from the back surface)

Step 2: Find the net darg force.

∴

Net force drag force = mnA

[{(v + v_{0})}^{2} - {(v - v_{0})}^{2}]

[from front]

= m n A (4 v v_{0}) = (4 m n A v) v_{0}

= (4 ρ A v) v_{0}

where we have assumed,

ρ = \frac{m N}{V} = \frac{M}{V}

If v = velocity along x-axis,

Then, we can write,

K E = \frac{1}{2} m v^{2} = \frac{1}{2} k_{B} T

\Rightarrow v = \sqrt{\frac{k_{B} T}{m}} [K_{B} = B o l z m a n n c o n s \tan t]

K E = K i n e t i c e n e r g y

T = T e m p e r a t u r e

∴

From Eq.(i), Drag force=

4 ρ A \sqrt{\frac{k_{B} T}{m}} v_{0}

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions