Ncert Exercises & Solutions

Q. 30 Show the nature of the following graphs for a satellite orbiting the Earth.

(a) KE versus orbital radius R

(b) PE versus orbital radius R

Hint: The gravitational force provides the required centripetal force for the satellite.

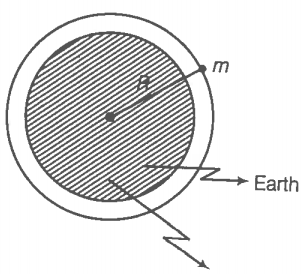
Consider the diagram, where a satellite of mass m is moving around the earth in a circular orbit of radius R.

Step 1: Find the kinetic energy of the satellite.

The orbital speed of the satellite orbiting the earth is given by,

v_{0} = \sqrt{\frac{G M}{R}}

$v_{0} = \sqrt{\frac{G M}{R}}$

where M and R are the mass and radius of the earth.

(a)

∴

$∴$ KE of a satellite of mass m,

E_{K} = \frac{1}{2} m v_{0}^{2} = \frac{1}{2} m \times \frac{G M}{R}

$E_{K} = \frac{1}{2} m v_{0}^{2} = \frac{1}{2} m \times \frac{G M}{R}$

E_{K} \propto \frac{1}{R}

$E_{K} \propto \frac{1}{R}$

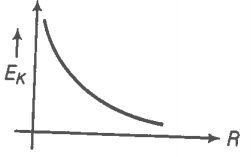
lt means the KE decreases exponentially with radius.

The graph for KE versus orbital radius R is shown in the figure.

Step 2: Find the potential energy of the satellite.

(b) Potential energy of a satellite,

E_{p} = - \frac{G M m}{R}

$E_{p} = - \frac{G M m}{R}$

E_{p} \propto - \frac{1}{R}

$E_{p} \propto - \frac{1}{R}$

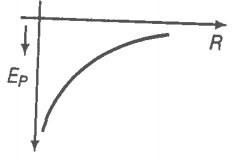
The graph for PE versus orbital radius R is shown in the figure.

Step 3: Find the total energy of the satellite.

E = E_{K} + E_{p} = \frac{G M m}{2 R} - \frac{G M m}{R} = - \frac{G M m}{2 R}

$E = E_{K} + E_{p} = \frac{G M m}{2 R} - \frac{G M m}{R} = - \frac{G M m}{2 R}$

The graph for total energy versus orbital radius R is shown in the figure.