Hint: Apply Newton's law of gravitation.
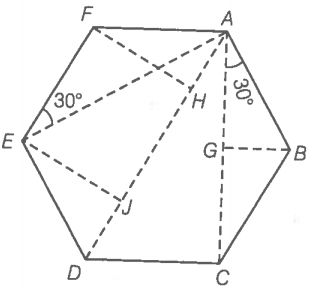
Consider the diagram below in which six point masses are Placed at six vertices A, B, C, D, E and F.
Step 1: Find the forces on any mass due to other masses.
Force on mass m at A due to mass m at B is, along with AB.
Force on mass m at A due to mass m at C is, along with AC.
Force on mass m at A due to mass mat D is, along with AD.
Force on mass m at A due to mass mat E is, along with AE.
Force on mass m at A due to mass m at F is, along with AF.
Step 2: Find the resultant force on mass m at A.
Resultant forces on mass m due to and along with AD.
Angle between ]
along with AD.
So the net force along AD