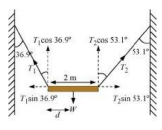
Question 7. 8. A non-uniform bar of weight W is suspended at rest by two strings of negligible weight as shown in Fig. The angles made by the strings with the vertical are 36.9° and ‘ 53.1° respectively. The bar is 2 m long. Calculate the distance d of the center of gravity of the bar from its left end.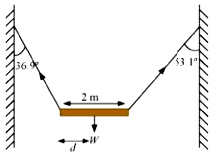

© 2026 GoodEd Technologies Pvt. Ltd.