Ncert Exercises & Solutions

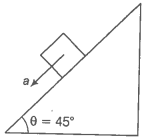
Q. 35 When a body slides down from rest along a smooth inclined plane making an angle of 45 $°$ $°$ with the horizontal, it takes time T. When the same body slides down from rest along a rough inclined plane making the same angle and through the same distance, it is seen to take time pT, where p is some number greater than 1. Calculate the coefficient of friction between the body and the rough plane.

Hint: Acceleration of body on rough incline plane decreases.

Step 1: Find the acceleration of the body on a smooth incline plane.

Consider the diagram where a body slides down from along an inclined plane of inclination

θ (= 45^{\circ})

$θ (= 45^{\circ})$

On Smooth inclined plane Acceleration Of a body sliding down a smooth inclined

\begin{matrix} a = g sin θ Here, θ = 45^{\circ} ∴ a = g sin 45^{\circ} = \frac{g}{\sqrt{2}} \end{matrix}

$\begin{array}{l} a = g \sin θ \\ Here, θ = 45^{\circ} \\ ∴ a = g \sin 45^{\circ} = \frac{g}{\sqrt{2}} \end{array}$

Step 2: Find the length (s) of the incline plane

Let the traveled distance be

Using the equation of motion.

s = ut + \frac{1}{2} {at}^{2}, we get

$s = ut + \frac{1}{2} {at}^{2}, we get$

\begin{matrix} s = \frac{1}{2} \frac{g}{\sqrt{2}} T^{2} or s = \frac{{gT}^{2}}{2 \sqrt{2}} \end{matrix}

$\begin{array}{l} s = \frac{1}{2} \frac{g}{\sqrt{2}} T^{2} \\ or s = \frac{{gT}^{2}}{2 \sqrt{2}} \end{array}$

Step 3: Find the acceleration of the body on the rough inclined plane.

On rough inclined plane Acceleration of the body

a = g (sin θ - μ cos θ)

$a = g (\sin θ - μ \cos θ)$

\begin{matrix} = g (sin 45^{\circ} - μcos 45^{\circ}) = \frac{g (1 - μ)}{\sqrt{2}} (As, sin 45^{\circ} = cos 45^{\circ} = \frac{1}{\sqrt{2}}) \end{matrix}

$\begin{array}{l} = g (\sin 45^{\circ} - μcos 45^{\circ}) \\ = \frac{g (1 - μ)}{\sqrt{2}} (As, \sin 45^{\circ} = \cos 45^{\circ} = \frac{1}{\sqrt{2}}) \end{array}$

Step 4: Find the coefficient of friction by applying the equation of motion.
Again using the equation of motion,

s = ut + \frac{1}{2} {at}^{2}, we get

$s = ut + \frac{1}{2} {at}^{2}, we get$

\begin{matrix} S = 0 (pT) + \frac{1}{2} \frac{g (1 - μ)}{\sqrt{2}} (ρT)^{2} or S = \frac{g (1 - μ) p^{2} T^{2}}{2 \sqrt{2}} . . . (ii) \end{matrix}

$\begin{array}{l} S = 0 (pT) + \frac{1}{2} \frac{g (1 - μ)}{\sqrt{2}} (ρT)^{2} \\ or S = \frac{g (1 - μ) p^{2} T^{2}}{2 \sqrt{2}} . . . (ii) \end{array}$
From Eqs. (i) and (ii), we get

\begin{matrix} \frac{{gT}^{2}}{2 \sqrt{2}} = \frac{g (1 - μ) p^{2} T^{2}}{2 \sqrt{2}} or (1 - μ) p^{2} = 1 or 1 - μ = \frac{1}{p^{2}} or μ = (1 - \frac{1}{p^{2}}) \end{matrix}

$\begin{array}{l} \frac{{gT}^{2}}{2 \sqrt{2}} = \frac{g (1 - μ) p^{2} T^{2}}{2 \sqrt{2}} \\ or (1 - μ) p^{2} = 1 \\ or 1 - μ = \frac{1}{p^{2}} \\ or μ = (1 - \frac{1}{p^{2}}) \end{array}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions