Ncert Exercises & Solutions

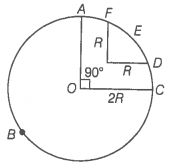
Q. 37 A racing car travels on a track (without banking) ABCDEFA. ABC is a circular arc of radius 2 R. CD and FA are straight paths of length R and DEF is a circular arc of radius R = 100 m. The coefficient of friction on the road is $μ$ $μ$ = 0.1. The maximum speed of the car is 50 m/s. Find the minimum time for completing one round.

Hint: Balance frictional force with centripetal force for the circular path.

Step 1: Find maximum speed of the car on the circular path.

Balancing frictional force with centripetal force

\frac{{mv}^{2}}{r} = f = μN = μmg

$\frac{{mv}^{2}}{r} = f = μN = μmg$

where N is normal reaction.

∴ v = \sqrt{μrg} (where, r is radius of the circular track)

$∴ v = \sqrt{μrg} (where, r is radius of the circular track)$

Step 2: Find the time taken for path ABC.

For path ABC,

path length = \frac{3}{4} (2 π 2 R) = 3 πR = 3 π \times 100

$path length = \frac{3}{4} (2 π 2 R) = 3 πR = 3 π \times 100$

$\begin{array}{l} = 300 πm \\ v_{1} = \sqrt{μ 2 Rg} = \sqrt{0 .1 \times 2 \times 100 \times 10} \\ = 14 .14 m / s \\ ∴ t_{1} = \frac{300 π}{14 .14} = 66 .6 s \end{array}$

Step 3: Find the time taken for path DEF.

$For path DEF, path length = \frac{1}{4} (2 πR) = \frac{π \times 100}{2} = 50 π$

$v_{2} = \sqrt{μAg} = \sqrt{0 .1 \times 100 \times 10} = 10 m / s$

$t_{2} = \frac{50 π}{10} = 5 πs = 15 .7 s$

$Step 4 : Find time taken for path CD and FA .$

$For paths, CD and FA, path length = R + R = 2 R = 200 m$

$t_{3} = \frac{200}{50} = 4 .0 s$

$Step 5 : Find total time taken for completing one round .$

$\begin{array}{l} ∴ Total time for completing one round \\ t = t_{1} + t_{2} + t_{3} = 66 .6 + 15 .7 + 4 .0 = 86 .3 s . \end{array}$

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions