Ncert Exercises & Solutions

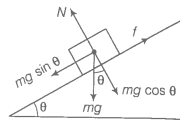
Q. 41 A rectangular box lies on a rough inclined surface. The coefficient friction between the surface and the box is $μ$ . Let the mass of the box be m.

(a) At what angle of inclination $θ$ of the plane to the horizontal will the box just start to slide down the plane?

(b) What is the force acting on the box down the plane, if the angle inclination of the plane is increased to $α$ > $θ$ ?

(c) What is the force needed to be applied upwards along the plane to make the box either remain stationary or just move up with uniform speed?

(d) What is the force needed to be applied upwards along the plane make the box move up the plane with acceleration a?

Hint: Frictional force,

μmgcosθ

acts on the box in the direction opposite to the direction of movement of the box.

Step 1: Find the angle of inclination,

θ

for the box to just starts sliding down the pane.

(a) Consider the adjacent diagram, force of friction on the box will act up the plane.

For the box to just starts sliding down

\begin{array}{l} mgsin θ = f = μN = μmgcosθ \\ or \tan θ = μ \Rightarrow θ = \tan^{- 1} (μ) \end{array}

Step 2: Find the force acting on the box down the plane, if the angle inclination of the plane is increased to

α

θ

(b) When angle of inclination is increased to

α > θ

, then net force acting on the box, down the plane is

\begin{array}{l} F_{1} = mgsin α - f = mgsin α - μN \\ = mg (\sin α - μcos α) \end{array}

Step 3: Find force needed to be applied upwards along the plane to make the box either remain stationary.

F_{2} = mgsin α + f = mg (\sin α + μcos α)

(In this case, friction would act down the plane).

Step 4: Find upward force needed to make the box move up the plane with acceleration a.

(d) If the box is to be moved with an upward acceleration a, then upward force needed

F_{3} = mg (\sin α + μ \cos α) + ma

NEET Information

courses

Company

Botany Questions

Chemistry Questions

Physics Questions

Zoology Questions